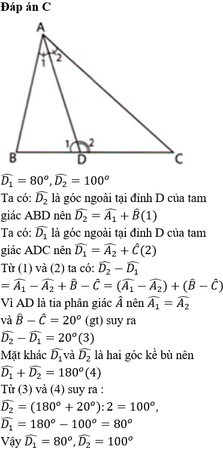
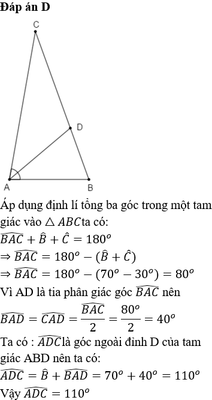
cho tam giác của góc A cắt BC tại D tính ADC bít rằng B - C = 40o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 2 2022
Xét tam giác ABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ \Rightarrow\widehat{A}=180^0-\widehat{B}-\widehat{C}\\ =180^0-70^0-30^0=80^0\\ Mà.AD,là.phân.giác.\widehat{BAC}\\ \Rightarrow\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{A}}{2}=\dfrac{80}{2}=40^0\)
TA
0
2 tháng 7 2015
b ) GÓC B = GÓC C
=> TAM GIÁC ABC CÂN TẠI A
=> AB = AC (ĐPCM)
a) XÉT 2 TAM GIÁC ADB VÀ ADC, CÓ:
AB = AC (THEO CÂU B)
AD LÀ CẠNH CHUNG
GÓC A1 = GÓC A2 (AD LÀ PHÂN GIÁC, GT)
=> TAM GIÁC ADB = ADC (C.G.C) (ĐPCM)
VT
18 tháng 12 2017
a) Xét tam giác adb và tam giác adc
ab = ac
góc a1 và góc a2 là cạnh chung
Suy ra tam giác adb = tam giác adc
b) Vì tam giác adb = tam giác adc
Nên AB = AC
M
16 tháng 7 2017
b, vì tam giác ABC có góc B =góc C => tam giác ABC là tam giác cân ( T/C tam giác cân )
do đó AB =AC
a, xét tam giác ABD và tam giác ACD có :
AB = AC ( CMT )
GÓC BAD = GÓC CAD ( VÌ AD LÀ PHÂN GIÁC CỦA GÓC A )
AD CHUNG
DO ĐÓ TAM GIÁC ABD = TAM GIÁC ACD ( C-G-C )
21 tháng 12 2017
a) vì góc B = góc C ( gt )
góc BAD = góc DAC ( p/g góc A )
=> 180o - ( góc B + góc BAD ) = 180o - ( góc C + góc DAC )
=> góc ADB = góc ADC
xét \(\Delta ADB\) và \(\Delta ADC\)có :
g : BÂD = DÂC ( AD là tia p/g góc A )
c : AD là cạnh chung
g : ADB = ADC ( cmt )
=> \(\Delta ADB=\Delta ADC\)( g - c - g ) ( đpcm )
b) Vì \(\Delta ADB=\Delta ADC\) => AB=AC ( 2 cạnh tương ứng ) ( đpcm )
W
15 tháng 3 2020
a) Xét tam giác ABC. Ta có:
Vì AD là tia phân giác của góc A nên:
\(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{A}}{2}=40^{^o}\)
\(\widehat{ADB}=180^o-70^o-40^o=70^o\)
Vì \(\widehat{ADB}=\widehat{ABD}=70^o\)nên ABD là tam giác cân.
b)Vì \(\widehat{ADB}\)kề bù với \(\widehat{ADC}\)nên \(\widehat{ADC}=180^o-70^o=110^o\)
Do tam giác ACD là tam giác nên \(\widehat{ACD}=180^o-40^o-110^o=30^o\)
c) Đặt đỉnh ngoài của B là B1.
Ta có: \(\widehat{B_1}=180^o-70^o=110^o\)