Giả sử đường thẳng y = x + m cắt đồ thị (C) của hàm số y = x − 1 1 − 2 x tại hai điểm phân biệt E và F. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với C tại E và F. Tìm giá trị nhỏ nhất minS của biểu thức S = k 1 4 + k 2 4 − 3 k 1 k 2 .
A. min S = − 1
B. min S = − 5 8
C. min S = 135
D. min S = − 25 81




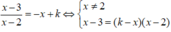
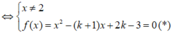

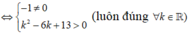
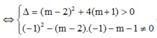
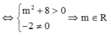






Đáp án A.
Phương trình hoành độ giao điểm của đồ thị (C) với đường thẳng đã cho là
x − 1 1 − 2 x = x + m ⇔ x − 1 = 1 − 2 x x + m
(do x = 1 2 không là nghiệm)
⇔ 2 x 2 + 2 m x − m − 1 = 0 (*).
Đồ thị (C) với đường thẳng đã cho cắt nhau tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt ⇔ m 2 + 2 m + 2 > 0 (nghiệm đúng với mọi m).
Giả sử E x 1 ; y 1 , F x 2 ; y 2 thì x 1 , x 2 là hai nghiệm của (*).
Suy ra x 1 + x 2 = − m ; x 1 x 2 = − m + 1 2 .
Do đó 2 x 1 − 1 2 x 2 − 1 = 4 x 1 x 2 − 2 x 1 + x 2 + 1 = − 1 .
Ta có
k 1 = − 1 2 x 1 − 2 2 ; k 2 = − 1 2 x 2 − 1 2
nên k 1 k 2 = 1 .
Suy ra S ≥ 2 k 1 2 k 2 2 − 3 k 1 k 2 = − 1 . Dấu bằng xảy ra khi k 1 = − 1 k 2 = − 1 ⇒ x 1 = 0 x 2 = 1 hoặc x 1 = 1 x 2 = 0 ⇒ m = − 1 . Vậy S đạt giá trị nhỏ nhất bằng ‒1.