Tìm x, biết: x : − 2 5 = − 15 16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
5 tháng 1 2019
Đúng(0)
Những câu hỏi liên quan
O
23 tháng 3 2022
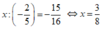
a) \(\dfrac{x}{-6}=\dfrac{-15}{45}\)
\(\dfrac{-x}{6}=\dfrac{-15}{45}\)
\(\dfrac{x}{6}=\dfrac{15}{45}\)
\(x=\dfrac{\left(15\cdot6\right)}{45}\)
\(x=2\)
b) \(\dfrac{x}{5}=\dfrac{16}{25}\)
\(x=\dfrac{\left(16\cdot5\right)}{25}\)
\(x=\dfrac{80}{25}\)
\(x=\dfrac{16}{5}\)
c) \(\dfrac{5}{x-3}=\dfrac{20}{-12}\)
\(x-3=\dfrac{\left(5\cdot-12\right)}{20}\)
\(x-3=-3\)
\(x=\left(-3\right)+3\)
\(x=0\)
d) \(\dfrac{2}{5}\cdot x=\dfrac{6}{35}\)
\(x=\dfrac{6}{35}\div\dfrac{2}{5}\)
\(x=\dfrac{3}{7}\)
NH
1
14 tháng 1 2021
x + 5 x 2 - ( 32 + 16 x 3 : 6 - 15 ) = 0
x + 5 x 2 - 25 = 0
x + 5 x 2 = 0 + 25
x + 5 x 2 = 25
x + 10 = 25
x = 25 - 10
x = 15
2 tháng 3 2022
\(a)x=\dfrac{1}{4}+\dfrac{5}{13}=\dfrac{33}{52}.\\ b)\dfrac{x}{3}=\dfrac{2}{3}+\dfrac{-1}{7}.\\ \Leftrightarrow\dfrac{x}{3}=\dfrac{11}{21}.\\ \Leftrightarrow\dfrac{7x}{21}=\dfrac{11}{21}.\\ \Rightarrow7x=11.\\ \Leftrightarrow x=\dfrac{11}{7}.\\ c)\dfrac{x}{3}=\dfrac{16}{24}+\dfrac{24}{36}=\dfrac{2}{3}+\dfrac{2}{3}=\dfrac{4}{3}.\\ \Rightarrow x=4.\\ d)\dfrac{x}{15}=\dfrac{1}{5}+\dfrac{2}{3}=\dfrac{13}{15}.\\ \Rightarrow x=13.\)
TH
4
LT
6 tháng 3 2020
suy ra3.(5x-1) - 4.(5x-1) + 6(5x-1) =15
suy ra 5.(5x-1) = 15
suy ra 5x-1=3
suy ra x=4/5
6 tháng 3 2020
\(\Leftrightarrow3\left(5x-1\right)-4\left(5x-1\right)+6\left(5x-1\right)=15\)
\(\Leftrightarrow\left(3-4+6\right)\left(5x-1\right)=15\)
\(\Leftrightarrow5\left(5x-1\right)=15\)
\(\Leftrightarrow5x-1=\frac{15}{5}=3\)
\(\Leftrightarrow5x=3+1=4\)
\(\Leftrightarrow x=\frac{4}{5}\)
Vậy \(x=\frac{4}{5}\)
HN
2
O
2 tháng 2 2017
-16 + 23 + x = -16
7 + x = -16
x = -16 - 7
x = -23
2x + 35 = -15
2x = -15 - 35
2x = -50
x = -25
-13 x |x | = -26
x = -26 : (-13)
x = 2
Vậy x = 2 hoặc -2
|2x - 5| = 13
2x = 13 + 5
2x = 18
x = 9
(x - 3) x (x + 2) = 0
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x+2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-2\end{cases}}\)
2 tháng 2 2017
2)2x+35=-15
2x =-15-35
2x = -50
x =-25
1)-16+23+x=-16
7+x =-16
x =-16-7
x =-23
3)-13 * lxl =-26
lxl = -26:-13
lxl =2
<=>x=-2 hoac x=2
5) (x-3).(x+2) =0
<=>\(\orbr{\begin{cases}x-3=0\\x+2=0\end{cases}}\) <=>\(\orbr{\begin{cases}x=3\\x=-2\end{cases}}\)