Thời gian và vận tốc của một vật khi nó đang trược xuống mặt phẳng nghiêng được xác định bởi công thức ∫ 2 20 - 3 v d v (giây). Chọn gốc thời gian là lúc vật bắt đầu chuyển động. Hãy tìm phương trình vận tốc.
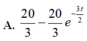
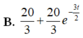
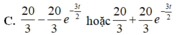
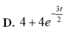
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có t = ∫ 2 20 - 3 v d x = - 2 3 ln 20 - 3 v + C với C là hằng số
Vào thời điểm t = 0 thì vật có vận tốc bằng 0. Suy ra
0 = - 2 3 ln 20 + C ⇔ C = 2 3 ln 20
Khi đó
t = - 2 3 ln 20 - 3 v + 2 3 ln 20 ⇔ ln 20 - 3 v = ln 20 - 3 2 t ⇔ 20 - 3 v = 20 e - 3 2 t ⇔ 20 - 3 v = 20 e - 3 2 t 20 - 3 v = - 20 e - 3 2 t ⇔ v = 20 3 - 20 3 e - 3 2 t v = 20 3 + 20 3 e - 3 2 t
Để ý rằng phương trình thứ hai không thể đạt v = 0 tại t = 0 cho nên ta chỉ nhận phương trình thứ nhất là 20 3 - 20 3 - 3 t 2
Đáp án A

a) Khi vật nằm yên trên mặt phẳng nghiêng thì hợp lực tác dụng lên vật bằng không, ứng với góc α lớn nhất ta có:
mgsinα = μmgcosα tan α = μ = 0,45 và α ≈ 24 °.


$[v(t) = \frac{ds(t)}{dt} = \frac{d}{dt}(2t^3+4t+1)]$
$[a(t) = \frac{dv(t)}{dt} = \frac{d}{dt}(6t^2 + 4)]$
$[a(t) = 12t]$
Khi (t = 1), ta có:
$[v(1) = 6(1)^2 + 4 = 10 , \text{m/s}]$4
$[a(1) = 12(1) = 12 , \text{m/s}^2]$
Vậy, khi (t = 1), vận tốc của vật là 10 m/s và gia tốc của vật là $12 m/s$

Chọn B
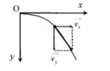
v x = v 0 v y = g t ⇒ v = v x 2 + v y 2 = v 0 2 + g 2 t 2

Ta có:
+ Theo phương Ox: v x = v 0
+ Theo phương Oy: v y = g t
Độ lớn của vận tốc tại vị trí bất kì: v = v x 2 + v y 2 = v 0 2 + g 2 t 2
Đáp án: B

Chọn đáp án B
Ta có ![]()
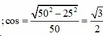
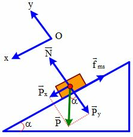
Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
Vật chịu tác dụng của các lực ![]()
Theo định luật II newton ta có: ![]()
Chiếu Ox ta có:
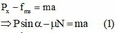
Chiếu Oy: ![]()
Thay (2) vào (1)
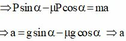
![]()
Vì bắt đầu trượt nên ![]()
Áp dụng: 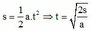
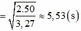
![]()
![]()

Ta có sin α = 25 50 = 1 2 ; c o s = 50 2 − 25 2 50 = 3 2
Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
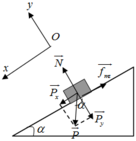
Vật chịu tác dụng của các lực N → ; P → ; f → m s
Theo định luật II newton ta có: N → + P → + f → m s = m a →
Chiếu Ox ta có: P x − f m s = m a ⇒ P sin α − μ N = m a 1
Chiếu Oy: N = P y = P cos α ( 2 )
Thay (2) vào (1) ⇒ P sin α − μ P cos α = m a
⇒ a = g sin α − μ g cos α
⇒ a = 10. 1 2 − 0 , 2.10 3 2 = 3 , 27 m / s 2
Vì bắt đầu trượt nên v 0 = 0 m / s
Áp dụng: s = 1 2 a . t 2 ⇒ t = 2 s a = 2.50 3 , 27 ≈ 5 , 53 s
Mà v = v 0 + a t = 0 + 3 , 27.5 , 53 = 18 , 083 m / s

Đầu tiên, chúng ta xác định lực ma sát trượt giữa vật và mặt phẳng nghiêng. Lực ma sát trượt được tính bằng công thức:
F_friction = μ * N
Trong đó:
F_friction là lực ma sát trượt.μ là hệ số ma sát giữa vật và mặt phẳng nghiêng.N là lực phản xạ của mặt phẳng nghiêng lên vật, được tính bằng công thức N = m * g * cos(α), với m là khối lượng của vật, g là gia tốc trọng trường và α là góc nghiêng của mặt phẳng.Tiếp theo, chúng ta xem xét lực hướng lên của vật (lực N) và lực hướng xuống của vật (lực trọng trường m * g * sin(α)). Vì vật được đẩy từ thấp lên cao, nên lực hướng lên sẽ lớn hơn lực hướng xuống:
N > m * g * sin(α)
Chúng ta biết rằng thời gian đẩy vật lên nhỏ gấp n lần thời gian đẩy vật xuống, vậy ta có:
N * n = m * g * sin(α)
Thay N = m * g * cos(α) vào biểu thức trên, ta có:
m * g * cos(α) * n = m * g * sin(α)
Simplify và loại bỏ m, g:
cos(α) * n = sin(α)
Từ đó, ta có:
μ = tan(α)
Vậy, hệ số ma sát μ giữa vật và mặt phẳng nghiêng là bằng giá trị của hàm tan(α).
Đáp án A