Để bất phương trình x - 6 1 - x m - 1 6 x - 2 6 x + 2 m + 1 ≥ 0 thỏa mãn với mọi x thuộc đoạn 0 ; 1
A. m ≥ 1 4
B. m ≤ 1 2
C. 1 4 ≤ m ≤ 1 2
D. m ≤ 1 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
+ TH1: Với m> - 2 , bất phương trình (*) trở thành: 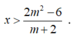
Tập nghiệm của bất phương trình là 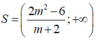
Để bất phương trình đã cho nghiệm đúng với mọi x < 1thì 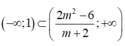
Suy ra không ra giá trị nào của m thỏa mãn.
+ TH2: m = -2, bất phương trình (*) trở thành: 0x > 2
Bất phương trình vô nghiệm
+ TH3: Với m< - 2 , bất phương trình (*) trở thành: 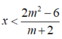
Tập nghiệm của bất phương trình là 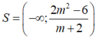
Để bất phương trình đã cho nghiệm đúng với mọi x< 1thì 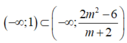
Hay 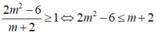
Kết hợp điều kiện m < -2 không có m
Vậy không có m thỏa mãn.

d: \(\Delta=m^2-2m+1-4m\left(m-1\right)=m^2-2m+1-4m^2+4m=-3m^2+2m+1\)
Để bất phương trình có nghiệm đúng với mọi x thì \(\left\{{}\begin{matrix}-3m^2+3m-m+1< 0\\m< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(-3m+1\right)< 0\\m< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(3m-1\right)>0\\m< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>1\\m< \dfrac{1}{3}\end{matrix}\right.\\m< 0\end{matrix}\right.\Leftrightarrow m< 0\)

2.
b, \(-4< \dfrac{2x^2+mx-4}{-x^2+x-1}< 6\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4< \dfrac{2x^2+mx-4}{-x^2+x-1}\left(1\right)\\\dfrac{2x^2+mx-4}{-x^2+x-1}< 6\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow4\left(x^2-x+1\right)>2x^2+mx-4\)
\(\Leftrightarrow2x^2-\left(m+4\right)x+8>0\)
Yêu cầu bài toán thỏa mãn khi \(\Delta=m^2+8m-48< 0\Leftrightarrow-12< m< 4\)
\(\left(2\right)\Leftrightarrow-6\left(x^2-x+1\right)< 2x^2+mx-4\)
\(\Leftrightarrow8x^2+\left(m-6\right)x+2>0\)
Yêu cầu bài toán thỏa mãn khi \(\Delta=m^2-12m-28< 0\Leftrightarrow-2< x< 14\)
Vậy \(m\in\left(-2;4\right)\)
2.
a, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-4\right)x^2+\left(1+m\right)x+2m-1>0\) có nghiệm đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m-4>0\\\Delta=m^2+2m+1-4\left(m-4\right)\left(2m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>4\\\left[{}\begin{matrix}m< \dfrac{3}{7}\\m>5\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow m>5\)

Đặt ![]()
Suy ra ![]()
Ta có ![]()
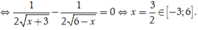
Ta có bảng biến thiên
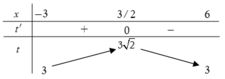
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
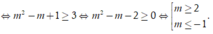
Chọn C.
Chọn B
Phương pháp: Đánh giá.
Cách giải: Với x=1 dễ thấy bất phương trình thỏa mãn với mọi m
Do đó yêu cầu bài toán tương đương với