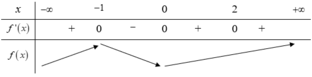
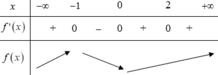
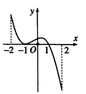
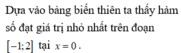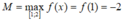Cho hàm số xác định với mọi giá trị của thuộc .
Nếu giá trị của biến tăng lên mà giá trị tương ứng của cũng tăng lên thì hàm được gọi là hàm số trên .
Nếu giá trị của biến tăng lên mà giá trị tương ứng của lại giảm đi thì hàm được gọi là hàm số trên .
đồng biếnnghịch biến(Kéo thả hoặc click vào để điền)
 Câu hỏi 2 (0.25 điểm)
Câu hỏi 2 (0.25 điểm)Hàm số là hàm đồng biến hay nghịch biến?
Đồng biến.Nghịch biến. Câu hỏi 3 (0.5 điểm)
Câu hỏi 3 (0.5 điểm)Trong các hàm số sau đây, những hàm nào là hàm số bậc nhất?
 Câu hỏi 4 (0.5 điểm)
Câu hỏi 4 (0.5 điểm)Hàm số bậc nhất xác định với mọi giá trị của thuộc và có tính chất:
- Đồng biến trên , khi .
- Nghịch biến trên , khi .
(Kéo thả hoặc click vào để điền)
 Câu hỏi 5 (1 điểm)
Câu hỏi 5 (1 điểm)Cho hàm số bậc nhất: . Tìm hệ số , biết rằng khi thì
Trả lời:
.
 Câu hỏi 6 (1 điểm)
Câu hỏi 6 (1 điểm)Cho ba đường thẳng:
; ; .
Tìm giá trị của sao cho ba đường thẳng đồng quy tại một điểm.
Trả lời:
.
 Câu hỏi 7 (1 điểm)
Câu hỏi 7 (1 điểm)Góc tạo bởi đường thẳng y = ax + b và trục hoành là góc nào?
αββ hoặc α Câu hỏi 8 (1 điểm)
Câu hỏi 8 (1 điểm)Góc tạo bởi đường thẳng với trục Ox bằng:
30o.135o.45o.60o. Câu hỏi 9 (1 điểm)
Câu hỏi 9 (1 điểm)Điểm đối xứng với điểm M(-7 ; -2) qua trục Oy là điểm A'( ; )
 Câu hỏi 10 (0.5 điểm)
Câu hỏi 10 (0.5 điểm)Khoảng cách giữa hai điểm và là:
 Câu hỏi 11 (1 điểm) Cách chứng minh nhiều điểm cùng nằm trên một đường tròn
Câu hỏi 11 (1 điểm) Cách chứng minh nhiều điểm cùng nằm trên một đường trònCho và M là trung điểm BC. Hạ MD, ME theo thứ tự vuông góc với AB và AC. Trên tia BD và CE lần lượt lấy các điểm I, K sao cho D là trung điểm của BI, E là trung điểm CK. Chứng minh rằng bốn điểm B, I, K, C cùng nằm trên một đường tròn.
Bài giải:
+) M thuộc trung trực BI nên = MB = BC ⇔ vuông tại I ⇔ I thuộc đường tròn đường kính . (1) +) ME thuộc trung trực của CK nên = MC = BC ⇔ vuông tại K ⇔ K thuộc đường tròn đường kính BC. (2) Từ (1), (2) suy ra bốn điểm B, I, K, C cùng nằm trên đường đường kính BC. |
(Kéo thả hoặc click vào để điền)
 Câu hỏi 12 (1 điểm)
Câu hỏi 12 (1 điểm)Cho tam giác ABC vuông tại A, điểm D thuộc AB, điểm E thuộc AC. Gọi M, N, P, Q theo thứ tự là trung điểm của DE, DC, BC, BE.
Chọn các khẳng định đúng.
MNPQ là hình chữ nhật.M, N, P, Q cùng thuộc một đường tròn.M, N, P, Q không cùng thuộc một đường tròn.MNPQ là hình vuông. Câu hỏi 13 (1 điểm)
Câu hỏi 13 (1 điểm)Tứ giác ABCD không là hình chữ nhật có góc B và góc D vuông.
A, B, C, D cùng thuộc đường tròn đường kính ACBD.
AC <=> BD. help cần gấp