Hai nguồn sóng kết hợp S 1 , S 2 trên mặt chất lỏng cách nhau a = 2 m dao động điều hòa cùng pha, phát ra hai sóng có bước sóng 1 m. Điểm A trên mặt chất lỏng nằm cách S 1 một khoảng d và A S 1 ⊥ S 1 S 2 . Giá trị cực đại của d để tại A có được cực đại của giao thoa là.
A. 2,5 m
B. 1 m
C. 2 m
D. 1,5 m






Đáp án D
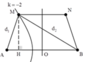
Cách 1: vẽ hình ra: ta thấy ngay: để tại A là cực đại giao thoa, đồng thời đoạn d lớn nhất
thì A chính là giao của hypebol vân cực đại thứ nhất với đường thẳng vuông góc S 1 S 2 q u a S 1
Khi đó, ta có: A S 2 - A S 1 = 1 × λ ⇔ d 2 + 4 - d = 1
⇒ d = 1 , 5 m
Cách 2: dùng kiến thức hypebol
lập pt hệ trục tọa độ Oxy với O là trung điểm của S 1 S 2
khi đó, điểm A thuộc đường thẳng x = 1 và đồng thời thuộc hypebol vân cực đại thứ nhất.
pt hybpebol: x 2 a 2 - y 2 b 2 = 1
Trong đó:
a = λ 2 = 0 , 5 ; b 2 = c 2 - a 2 = O S 1 2 - a 2 = 1 2 - 0 , 5 2 = 0 , 75 ; x = 1 ; y = d
Như vậy, tính được ngay: d = 1,5 m.