Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Côsin góc giữa mặt bên và mặt đáy là:
A. 1 3
B. 1 3
C. 1 2
D. 1 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 1 2018
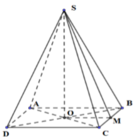
Gọi M là trung điểm của BC. Ta có: O M ⊥ B C S O ⊥ B C ⇒ B C ( S O M )
⇒ B C ⊥ S M
Ta có:
S B C ⊥ A B C D = B C S S B C ⊃ S M ⊥ B C ( A B C D ) ⊃ O M ⊥ B C ⇒ ∠ S B C , A B C D = ∠ S M ; O M = ∠ S M O
ABCD là hình vuông cạnh a ⇒ O B = 1 2 B D = a 2 2
∆ S O B vuông tại O ⇒ S O = S B 2 - O B 2
= a 2 - a 2 2 = a 2 2
O M = A B 2 = a 2 . ∆ S O M vuông tại O
⇒ tan S M O = S O O M = a 2 2 a 2 = 2
Vậy, cos ∠ S B C , A B C D = 1 3
Chọn đáp án A.
Phương pháp:
Xác định góc giữa hai mặt phẳng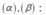
- Tìm giao tuyến ∆ của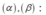
- Xác định 1 mặt phẳng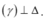
- Tìm các giao tuyến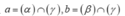
- Góc giữa hai mặt phẳng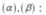
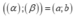
Cách giải:
Gọi M là trung điểm của BC. Ta có:
ABCD là hình vuông cạnh a
∆ SOB vuông tại O
Chọn: A