Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi
V
1
là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết
V
1
V
=
20
27
. Tỉ số
S
M
S
B
bằng: A.
2
3
B.
1
2
C.
3
4
D.
...
Đọc tiếp
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi V 1 là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết V 1 V = 20 27 . Tỉ số S M S B bằng:
A. 2 3
B. 1 2
C. 3 4
D. 4 5
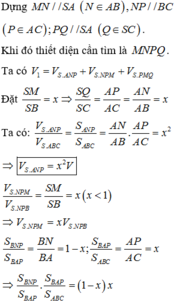
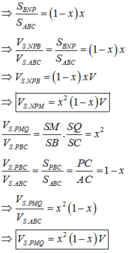
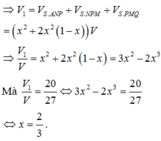
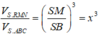
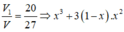
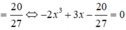
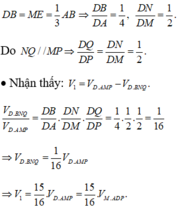
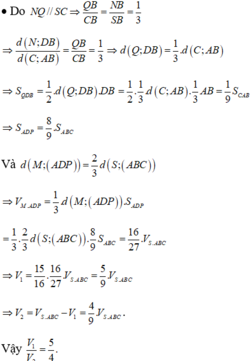
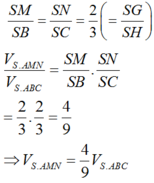
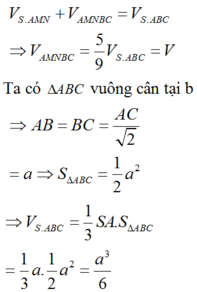
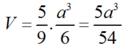
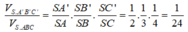
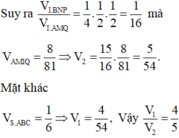
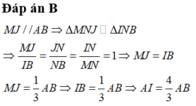
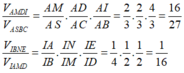
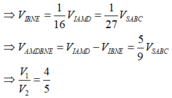
Phương pháp:
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác
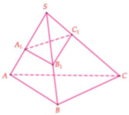
(Công thức Simson): Cho khối chóp S.ABC, các điểm A 1 , B 1 , C 1
lần lượt thuộc SA, SB, SC. Khi đó,
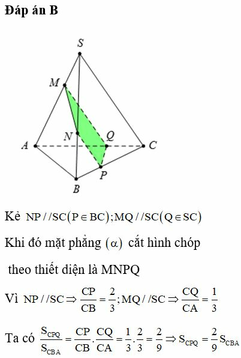
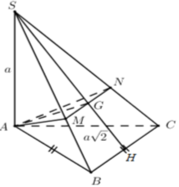
Cách giải:
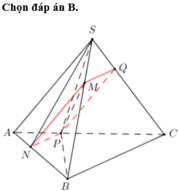
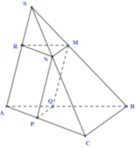
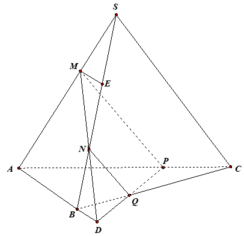
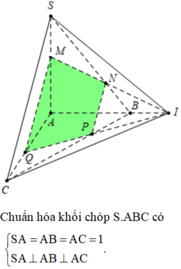
Dựng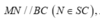
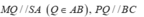
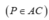
=> MNPQ là thiết diện cần dựng.
V i là thể tích khối đa giác SNM.APQ
Khi đó, khối đa giác SNM.APQ được chia làm 2 phần:
khối chóp tam giác S.RMN và khối lăng trụ RMN.AQP.
Giả sử S M S B = x
Ta có: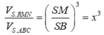
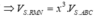
Mà V 1 V = 20 27
Chọn: A