Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
Mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 có tâm I (1;2;3), bán kính R=3.
IA = √6 < R nên A nằm trong mặt cầu.
Gọi r là bán kính đường tròn thiết diện, ta có 
Trong đó h là khoảng cách từ I đến (P).
Diện tích thiết diện là
Vậy diện tích hình tròn (C) đạt nhỏ nhất khi h = IA. Khi đó 
là véc tơ pháp tuyến của (P).
Phương trình mặt phẳng (P) là 1 (x-0)+2 (y-0)+ (z-2)=0 ó x + 2y + z – 2 = 0
Đáp án A
Mặt cầu (S) có tâm I(-1;4;-3) và có bán kính R = 6. Gọi H là hình chiếu vuông góc của I trên trục Ox. Ta có H(-1;0;0) và IH=5.
Gọi K là hình chiếu vuông góc của I trên mặt phẳng (P). Ta có
d(I; (P)) = IK ≤ IH = 5 < R = 6
Do đó mặt phẳng (P) luôn cắt mặt cầu (S) theo một đường tròn. Vậy không tồn tại mặt phẳng (P) chứa Ox và tiếp xúc với (S)
Chọn D
Mặt cầu (S) có tâm I (-1;3;-2) và bán kính R = √29.
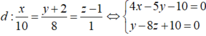
Mặt phẳng (P) chứa d có dạng m (4x-5y-10)+n (y-8z+10)=0
ó 4mx + (n – 5m)y – 8nz + 10n – 10m = 0 với m²+n²>0.
(P) tiếp xúc với (S) nên d (I, (P)) = R
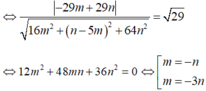
Trường hợp 1: m = -n, phương trình mặt phẳng (P): 2x-3y+4z-10=0.
Khi đó giao điểm của (P) và Ox có tọa độ là (0;0;5/2) (nhận)
Trường hợp 2: m = -3n, phương trình mặt phẳng (P):x-2y+6z-10=0.
Khi đó giao điểm của (P) và Ox có tọa độ là (0;0;5/3) (loại).
Đáp án D
Mặt cầu (S) có tâm I 1 ; − 2 ; 0 và bán kính R = 21
Đường thẳng Δ 1 có vtcp u 1 → = 2 ; − 3 ; 2 và đường thẳng Δ 2 có vtcp u 2 → = 1 ; 1 ; − 1
Mặt phẳng α có vtcp n → = u 1 → , u 2 → = 1 ; 4 ; 5 ⇒ α : x + 4 y + 5 z + m = 0
Do tiếp xúc với mặt cầu (S) nên
d I , α = 21 ⇔ 1 + 4. − 2 + 5.0 + m 1 2 + 4 2 + 5 2 = 21 ⇔ m = 7 + 21 2 m = 7 − 21 2
Do α cắt trục Oz tại điểm có cao độ dương ta có phương trình của α : x + 4 y + 5 z + 7 − 21 2 = 0
Đáp án A.