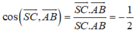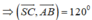Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a, BC = a 2 . Số đo góc giữa hai đường thẳng AB và SC bằng
A. 900.
B. 600.
C. 450.
D. 300.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
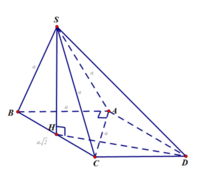
Cách 1. Xác định và tính góc giữa hai đường thẳng.
Tam giác ABC vuông tại A
![]()
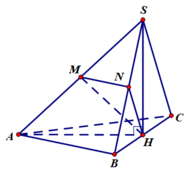
Do SA=SB=SC nên nếu gọi H là hình chiếu vuông góc của S lên (ABC) thì H là tâm đường tròn ngoại tiếp tam giác ABC mà tam giác ABC vuông tại A nên H là trung điểm của BC.
Dựng hình bình hành ABCD. Khi đó:(AB,SC)=(CD,SC) và CD=AB=a. Tam giác SBC vuông tại S
![]()
có SH là đường trùng tuyến nên SH= a 2 2
Tam giác CDH có
![]()
theo định lý Cô- Sin ta có
![]()
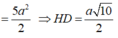
Tam giác SHD vuông tại H nên
![]()
Tam giác SCD có:
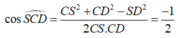
![]()
![]()
Cách 2. (Hay phù hợp với bài này) Ứng dụng tích vô hướng.
![]()
Theo giả thiết có
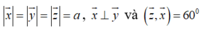
Ta có
![]()
![]()
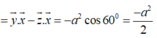
Suy ra:
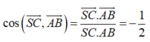
![]()
![]()

Chọn C
* Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABC), theo đầu bài SA=SB=SC và tam giác ABC vuông cân tại A ta có H là trung điểm của BC. Gọi M, N lần lượt là trung điểm của SA, SB ta có:


Đáp án là C
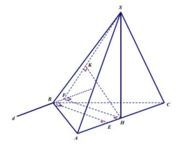
+) Từ giả thiết có AB = a, BC = a 2 , AC =a 3 , suy ra tam giác ABC vuông tại B .
+) Gọi H là trung điểm của AC .
+) Ta có
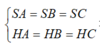
=> SH là trục đường tròn ngoại tiếp tam giác ABC => SH ⊥(ABC)
+) Kẻ đường thẳng d qua B và song song với AC .
+) Gọi ( α ) là mặt phẳng chứa SB và d
=> AC//( α ) => d(AC, SB) = d (AC,( α )) = d (H, ( α )) .
+) Kẻ HF ⊥ d , F ∈ d và kẻ HK⊥ SF, K ∈ SF
=> HK ⊥ ( α ) => d(H,( α )) =HK.
+) Kẻ BE⊥ AC , E ∈ AC .
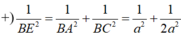
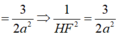
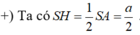


Cách 2: Toạ độ hoá

Áp dụng định lí Cosin
![]()
trong tam giác BSC, tam giác ASC ta dễ dàng tính được BC = a 2 , AC =a 3 . Suy ra tam giác ABC vuông tại B.
Gắn hệ trục Oxyz như hình vẽ khi đó tọa độ các điểm:
A(a;0;0), B(0;0;0), C(0;a 2 ;0), S a 2 ; a 2 2 ; a 2
(Trắc nghiệm)
Cho a = 2 thì A(2;0;0), C(0;2 2;0), S (1, 2,1), B(0;0;0).
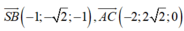
![]()
![]()
![]()
Khoảng cách


Đáp số bài toán là: d = a 22 11

Đáp án B
Gọi D là hình chiếu của S trên (ABC). Khi đó S D ⊥ A B C .
Do đó hình chiếu của SC trên (ABC) là CD. Suy ra góc giữa SC và (ABC) là S C D ^ .
Ta có B C ⊥ S C B C ⊥ S D ⇒ B C ⊥ C D , A B ⊥ S A A B ⊥ S D ⇒ A B ⊥ A D .
Vậy ABCD là hình chữ nhật.
Theo đề S C D ^ = 60 0 . Ta tính được B D = A C = a 5 , D S = C D 3 = a 3 .
Vậy S B = S D 2 + B D 2 = 8 a 2 = 2 a 2 .

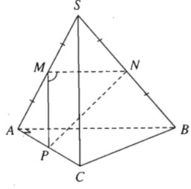
Gọi M, N, P lần lượt là trung điểm của SA, SB. AC. Để tính góc giữa hai đường thẳng SC và AB, ta cần tính ∠NMP.
Ta có:
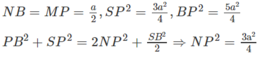
Mặt khác:
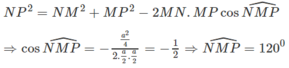
Vậy góc giữa hai đường thẳng SC và AB bằng 60 ο .
Chọn B.
Cách 1. Xác định và tính góc giữa hai đường thẳng
∆ ABC vuông tại A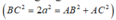
Do SA = SB = SC nên nếu gọi H là hình chiếu vuông góc của S lên (ABC) thì H là tâm đường trong ngoại tiếp tam giác ABC mà ∆ ABC vuông tại A nên H là trung điểm của BC. Dựng hình bình hành ABCD. Khi đó (AB;SC) = (CD;SC) và CD = AB = a
∆ SBC vuông tại S (vì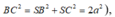 có SH là đường trung tuyến nên SH =
a
2
2
có SH là đường trung tuyến nên SH =
a
2
2
theo định lí Cô – Sin ta có
∆ SHD vuông tại H nên
∆ SCD có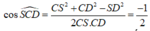
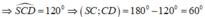
Cách 2. (Hay phù hợp với bài này) Ứng dụng tích vô hướng
Đặt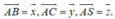 Theo giả thiết ta có:
Theo giả thiết ta có: 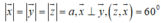
Ta có: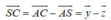
Xét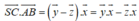

Suy ra: