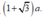Cho hình chóp đều S.ABC có AB = a, A S B ^ = 30 ° . Lấy các điểm B', C' lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác AB'C' nhỏ nhất. Tính chu vi đó.
A. ( 3 -1)a
B. 3 a
C. a 3 + 1
D. (1+ 3 )a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B

Ta có: A B ' + B ' C ' + C ' A = A B ' + B ' C ' + C ' D ≥ A D
Suy ra A,B’,C’,D thẳng hàng


Đáp án A.
Hướng dẫn giải:
Nếu a = b = c = 1 thì SA = SA',SB = SB',SC = SC'
nên ( A B C ) ≡ ( A ' B ' C ' )
Dễ thấy (A'B'C') đi qua trọng tâm của tam giác ABC
⇒ a + b + c = 3 là đáp án đúng
Chọn D.
Trải tứ chóp S.ABC ra mặt phẳng (SBC) thì chu vi tam giác AB'C' bằng
Dấu “=” xảy ra khi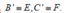
Ta có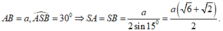
Lại có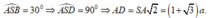
Vậy chu vi tam giác AB'C' đạt giá trị nhỏ nhất bằng