Tìm tất cả các giá trị của m để đường thẳng d : y = x + 4 cắt đồ thị hàm số
y
=
x
3
+
2
m
x
2
+
(
m
+
3
)
x
+
4
tại 3 điểm phân biệt
A
(
0
;
4
)
và C sao cho diện tích
∆
M
B
C
bằng 4, với M(1;3) A.
m
=
2
m
=
3
B.
m
=
-
2
m
=
...
Đọc tiếp
Tìm tất cả các giá trị của m để đường thẳng d : y = x + 4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + ( m + 3 ) x + 4 tại 3 điểm phân biệt A ( 0 ; 4 ) và C sao cho diện tích ∆ M B C bằng 4, với M(1;3)
A. m = 2 m = 3
B. m = - 2 m = 3
C. m = 3
D. m = - 3 m = - 2
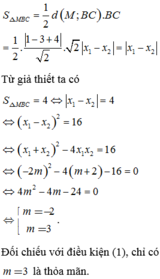
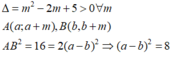
Đáp án C.
Phương trình có hoành độ giao điểm của d và (C):
x 3 + 2 m x 2 + ( m + 3 ) x + 4 = x + 4 ⇔ x 2 + 2 m x + ( m + 2 ) = 0
Để d cắt (C) tại 3 điểm phân biệt A(0;4) và C thì phương trình (*) phải có hai nghiệm phân biệt x 1 , x 2 khác 0
⇔ 0 2 + 2 m . 0 + m + 2 ≢ 0 ∆ ' = m 2 - m - 2 > 0 ⇔ m + 2 ≢ 0 ( m + 1 ) ( m - 2 ) > 0 ⇔ m ≢ - 2 m > 2 m < - 1 ⇔ m > 2 m < - 1 m ≢ - 2 (1)
Giả sử B x 1 ; x 1 + 4 và B x 2 ; x 2 + 4 với x 1 , x 2 là hai nghiệm của (*)
Suy ra B C = 2 x 1 - x 2 và theo định lí Vi-ét: x 1 + x 2 = - 2 m x 1 x 2 = m + 2
Ta có S ∆ M B C = 1 2 d ( M ; B C ) . B C = 1 2 . 1 - 3 + 4 2 . 2 x 1 - x 2 = x 1 - x 2
Từ giả thiết ta có S ∆ M B C = 4 ⇔ x 1 - x 2 = 4 ⇔ x 1 - x 2 2 = 16
⇔ x 1 + x 2 2 - 4 x 1 x 2 = 16 ⇔ ( - 2 m ) 2 - 4 ( m + 2 ) - 16 = 0 ⇔ 4 m 2 - 4 m - 24 = 0
m = - 2 m = 3 . Đối chiếu với điều kiện (1), chỉ có m = 3 là thỏa mãn