Cho phương trình z 4 + 2 z 2 − 8 = 0 có các nghiệm là z 1 ; z 2 ; z 3 ; z 4 . Tính giá trị biểu thức F = z 1 2 + z 2 2 + z 3 2 + z 4 2
A. F = 4
B. F = − 4
C. F = 2
D. F = − 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Gọi z = a + bi là nghiệm của phương trình.
Ta có: 4(a + bi) 2 + 8(a2 + b2) - 3 = 0
4(a2 – b2 + 2abi) + 8( a2 + b2) - 3 = 0
12a2 + 4b2 +8abi - 3 = 0
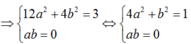
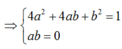

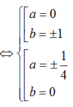
Vậy phương trình có 4 nghiệm phức.

Chọn D.
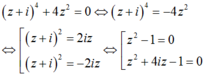
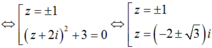
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.

Đáp án A
Phương pháp.
Giả sử ![]() Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa ![]() về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm 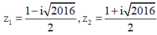
Giả sử ![]() . Từ
. Từ ![]() ta suy ra
ta suy ra
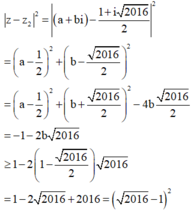
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của ![]() là
2016
-
1
là
2016
-
1
Đạt được khi và chỉ khi ![]()
Đáp án B.
Đặt t = z 2 ta được phương trình t 2 + 2 t − 8 = 0 (*)
Vì a c < 0 nên suy ra phương trình (*) có hai nghiệm phân biệt.
Suy ra z 1 2 = z 2 2 = t 1 ; z 3 2 = z 4 2 = t 2 .
Theo Vi-ét ta có t 1 + t 2 = − b a = − 2 .
Do đó F = z 1 2 + z 2 2 + z 3 2 + z 4 2 = 2 t 1 + t 2 = 2. − 2 = − 4 .