Tìm x thuộc Z biết: a , - 10 ≤ x ≤ - 7 b , 5 < x < 4 c ,

PT

Pham Trong Bach

8 tháng 4 2017

Tìm x thuộc Z biết: a , - 10 ≤ x ≤ - 7 b , 5 < x < 4 c , - 2 ⩽ x ⩽ 2 d , 1 2 < x < 2 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

1

CM

Cao Minh Tâm

8 tháng 4 2017

Đúng(0)

MT

Mai Tran

21 tháng 8 2017 - olm

Tìm x thuộc Z, biết

a, -5/7 + 1 + 30/-7 <_ x <_ -1/6 + 1/3 + 5/6

b, 1/2 - ( 1/3 + 1/4 ) < x < 1/48 - ( 1/16 - 1/6 )

c, ( x - 1/2 ) × ( x + 3/4 ) < 0

d, 3/( x + 2) × ( x + 5 ) + 5/( x+5 ) × ( x +10) + 7/( x+10) × ( x+17) = x/( x+2) × ( x+17)

#Hỏi cộng đồng OLM #Toán lớp 6

0

MT

Mai Tran

21 tháng 8 2017

Tìm x thuộc Z, biết

a, -5/7 + 1 + 30/-7 <_ x <_ -1/6 + 1/3 + 5/6

b, 1/2 - ( 1/3 + 1/4 ) < x < 1/48 - ( 1/16 - 1/6 )

c, ( x - 1/2 ) × ( x +3/4 ) < 0

d, 3/ ( x +2) ×( x +5) + 5/ ( x +5 ) × ( x+ 10) + 7/ ( x +10) ( x +17) = x / ( x+2) × ( x + 17)

#Hỏi cộng đồng OLM #Toán lớp 6

3

NM

NT Mai Hương

21 tháng 8 2017

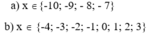
a, -5/7+ 1+ 30/-7< x < -1/6+ 1/3 +5/6
<=> -4< x <1
<=> x = -3; -2; -1; 0

Đúng(0)

KL

Khánh Linh

22 tháng 8 2017

a, \(\dfrac{-5}{7}+1+\dfrac{30}{-7}\le x\le\dfrac{-1}{6}+\dfrac{1}{3}+\dfrac{5}{6}\)
<=> -4 \(\le x\le1\)
Do x \(\in Z\Rightarrow x=-4;-3;-2;-1;0;1\)
b, \(\dfrac{1}{2}-\left(\dfrac{1}{3}+\dfrac{1}{4}\right)< x< \dfrac{1}{48}-\left(\dfrac{1}{16}-\dfrac{1}{6}\right)\)
<=> -\(\dfrac{1}{12}< x< \dfrac{1}{8}\)
Do x \(\in Z\Rightarrow x=0;1\)
@Mai Tran

Đúng(1)

CB

Chapi Beauty

23 tháng 1 2017 - olm

Giải đầy đủ hộ mình nhé :

Bài 1: Tìm x,y,;biết

a, x+y=2

b,y+z=3

c,z+x=-5

Bài 2 : Tìm x,y thuộc Z, biết (x-3).(y+2)=-5

Bài 3 : Tìm a thuộc Z, biết a.(a+2)<0

Bài 4 : Tìm x thuộc Z, sao cho (x^{2 -}4).(x²-10)<0

Bài 5 Tìm x thuộc Z, biết (x²-1).(x²-4)<0

#Hỏi cộng đồng OLM #Toán lớp 6

2

A

Ayatocute

23 tháng 1 2017

bài 2: (x-3).(y+2) = -5

Vì x, y \(\in\)Z => x-3 \(\in\)Ư(-5) = {5;-5;1;-1}

Ta có bảng:

x-3	5	-5	-1	1
y+2	1	-1	-5	5
x	8	-2	2	4
y	-1	-3	-7	3

bài 3: a(a+2)<0

TH1 : \(\orbr{\begin{cases}a< 0\\a+2>0\end{cases}}\)=>\(\orbr{\begin{cases}a< 0\\a>-2\end{cases}}\)=> -2<a<0 ( TM)

TH2: \(\orbr{\begin{cases}a>0\\a+2< 0\end{cases}}\Rightarrow\orbr{\begin{cases}a>0\\a< -2\end{cases}}\Rightarrow loại\)

Vậy -2<a<0

Đúng(0)

A

Ayatocute

23 tháng 1 2017

Bài 5: \(\left(x^2-1\right)\left(x^2-4\right)< 0\)

TH 1 : \(\hept{\begin{cases}x^2-1>0\\x^2-4< 0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x^2>1\\x^2< 4\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x>1\\x< 2\end{cases}}\)\(\Rightarrow\)1 < a < 2

TH 2: \(\hept{\begin{cases}x^2-1< 0\\x^2-4>0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x^2< 1\\x^2>4\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x< 1\\x>2\end{cases}}\)\(\Rightarrow\)loại

Vậy 1<a<2

Đúng(1)

CP

Chi Piu

8 tháng 1 2018 - olm

Bài 1 : Tìm x thuộc Z để :a) 3 < x < 5b) - 4 < x - 1 < 5c) - 8 < x + 2 < - 3Bài 2 : Tìm x thuộc Z để : a) | x + 7 | = 0b) | x + 10 | = x + 10 c) | x - 15 | = 15 - xd) ( x - 3 ) . ( x + 2 ) = 0Bài 3 : Tính :A = 8 + 8 mủ 2 + 8 mủ 3 + ... + 8 mủ 40 B = 4 - 4 mủ 2 + 4 mủ 3 - ... - 4 mủ 60 C = 1 - 2 mủ 4 + 2 mủ 8 - ... + 2 mủ 80Mong đc nhận sự ủng hộ của mọi người !Có gì mong mọi người giúp đỡ. Em xin chân thành cảm ơn ạ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

5

SG

Six Gravity

8 tháng 1 2018

Bài 1 :

A ) 3 < x < 5

=> x thuộc { 4 }

Vậy x = 4

Câu b và câu c cứ theo vậy mà làm .

Bài 2 :

| x + 7 | = 0

x = 0 - 7

x = -7

Vậy x = -7

Đúng(0)

S

ST

8 tháng 1 2018

Bài 1:

a, 3<x<5 => x=4

b, -4 < x - 1 < 5

=> x-1 thuộc {-3;-2;-1;0;1;2;3;4}

=> x thuộc {-2;-1;0;1;2;3;4;5}

c, -8 < x+2 < -3

=> x+2 thuộc {-7;-6;-5;-4}

=> x thuộc {-9;-8;-7;-6}

Đúng(0)

BD

bùi đức thắng

6 tháng 2 2017 - olm

tìm x thuộc z biết :

a) (-2).(7+x)<0

b)(x-1).(x+2)<0

c)(x^2-9).(2x+10)=0

d)(x-2)^2-25=0

#Hỏi cộng đồng OLM #Toán lớp 6

1

NH

Nguyễn Hà Giang

6 tháng 2 2017

a.-2 .(7 + x) < 0

ta có:- . + = - (khác 0)

- < 0

=>7 + x = -1;-2;-3;-4;...

x = -6;-5;-4;...

b.(x - 1) . (x + 2) < 0

ta có: - . + = - hoặc + . - = -

=>(x - 1) . ( x + 2) = -

=>x = -1

c.(x^2 - 9).(2x + 10) = 0

=> (x^2 - 9) = 0 hoặc (2x + 10) = 0

x^2 - 9 =0

x^2 =0 + 9

x^2 = 9

x = 3 hoặc -3

2x + 10=0

2x = 0 - 10

2x = -10
x = -10 : 2

x = -5

vậy: x thuộc {3;-3;5}

d.(x - 2)^2 - 25=0

(x - 2 )^2 = 0 + 25

(x - 2)^2 = 25

x - 2 =5

x = 5 + 2

x =7

Đúng(0)

HC

Hữu Cát

19 tháng 1 2017 - olm

Bài 1: tìm x thuộc Z biết:
a)(15-x)(-4-x)<0
b)(x-2)(7-x)>0
c)(x^2-13)(x^2=17)<0
Bài 2: Tìm a;b thuộc Z biết:
a.b=12 và a+b=-7

#Hỏi cộng đồng OLM #Toán lớp 6

1

VN

Vũ Như Mai

19 tháng 1 2017

Bài 1: Cho từng cái < hoặc > 0 rồi giải ra tìm điều kiện của x

Bài 2:

Phân tích số 12 ra là:

3 x 4 = 12

-3 x (-4) = 12

Ta thấy:

3 + 4 = 7

-3 + (-4) = -7 (đáp ứng đúng yêu cầu đề)

=> a = -3 và b = -4

Đúng(0)

CN

Cô Nhóc Năng Động

4 tháng 1 2018 - olm

A = 1 + 2 - 3 + 4 + 5 -6...+98-99

B = - 2 - 4 + 6 - 8 + 10 + 12 - ..... + 60
Bài 2 : Tìm x thuộc Z để :
a) | x | < 3
b) | x - 4 | < 3
c) | x + 10 | < 2
Bài 3 : Tìm a ; b thuộc Z để :
| a | + | b | = 1

#Hỏi cộng đồng OLM #Toán lớp 6

1

ND

nguyen duc thang

4 tháng 1 2018

Bài 2 :

a ) l x l < 3

=> l x l thuộc { 0 ; 1 ; 2 }

=> x thuộc { - 2 ; - 1 ; 0 ; 1 ; 2 }

Vậy x thuộc { - 2 ; - 1 ; 0 ; 1 ; 2 }

Đúng(0)

NN

Nguyễn Ngọc Khánh Linh

17 tháng 5 2020 - olm

Tìm x thuộc Z thỏa mãn :

a) 2/5 < x < 6/5

b) 3/5 < 3/x < 3/2

c) 3/8+ -11/8 < x < 22/9+5/18

d) -7/2+1/10+ -8/5<x< 1/2+ -5/6+ -5/4

Giải hộ em với ạ, đang cần gấp

Em cảm ơn

#Hỏi cộng đồng OLM #Toán lớp 6

1

HB

Hạt Bụi Thiên Thần

18 tháng 5 2020

a) 2/5 < x < 6/5

=> x = 1 ( =5/5 ) (vì x thuộc Z)

Vậy x = 1

b) 3/5 < 3/x < 3/2

=> 5 > x > 2

=> x thuộc { 4 ; 3 } (vì x thuộc Z)

Vậy ...

c) 3/8 + -11/8 < x < 22/9 + 5/18

=> -8/8 < x < 49/18

=>-1 < x < 2+13/18

=> x thuộc {0; 1; 2} ( vì x thuộc Z )

Vậy...

Đúng(0)

T

Trang

31 tháng 12 2016

1) Tìm x E Z biết: (x²-1).(x²- 4).(x² - 7).(x² - 10) < 0

2) Tìm Min A biết: A = |x - a| + |x - b| + |x - c| + |x - d| và a<b<c<d

#Hỏi cộng đồng OLM #Toán lớp 7

1

SG

soyeon_Tiểubàng giải

31 tháng 12 2016

1) (x^2 - 1)(x^2 - 4)(x^2 - 7)(x^2 - 10) < 0

<=> [(x^2 - 1)(x^2 - 10)][(x^2 - 4)(x^2 - 7)] < 0

<=> (x^4 - x^2 - 10x^2 + 10)(x^4 - 4x^2 - 7x^2 + 28) < 0

<=> (x^4 - 11x^2 + 10)(x^4 - 11x^2 + 28) < 0

=> x^4 - 11x^2 + 10 và x^4 - 11x^2 + 28 là 2 số trái dấu

Mà x^4 - 11x^2 + 10 < x^4 - 11x^2 + 28

Nên \(\left\{\begin{matrix}x^4-11x^2+10< 0\\x^4-11x^2+28>0\end{matrix}\right.\)\(\Leftrightarrow\left\{\begin{matrix}\left(x^2-\frac{11}{2}\right)^2-\frac{81}{4}< 0\\\left(x^2-\frac{11}{2}\right)^2-\frac{9}{4}>0\end{matrix}\right.\)\(\Leftrightarrow\frac{9}{4}< \left(x^2-\frac{11}{2}\right)^2< \frac{81}{4}\)

\(\Rightarrow\left[\begin{matrix}\frac{3}{2}< x^2-\frac{11}{2}< \frac{9}{2}\\-\frac{3}{2}>x^2-\frac{11}{2}>-\frac{9}{2}\end{matrix}\right.\)\(\Rightarrow\left[\begin{matrix}7< x^2< 10\\4>x^2>1\end{matrix}\right.\)

do \(x\in Z\Rightarrow x^2\in N\)=> x²= 9\(\Rightarrow\left[\begin{matrix}x=3\\x=-3\end{matrix}\right.\)

Vậy x = 3; x = -3

2) A = |x - a| + |x - b| + |x - c| + |x - d|

A = |x - a| + |x - b| + |c - x| + |d - x|\(\le\)

|x - a + x - b + c - x + d - x|= |c - a + d - b|

= c - a + d - b ( vì c - a > 0; d - b > 0)

Dấu "=" xảy ra khi \(\left\{\begin{matrix}x-a\ge0\\x-b\ge0\\x-c\le0\\x-d\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{\begin{matrix}a\le x\\b\le x\\c\ge x\\d\ge x\end{matrix}\right.\)

Vậy Min A = c - a + d - b khi \(\left\{\begin{matrix}a\le x\\b\le x\\c\ge x\\d\ge x\end{matrix}\right.\); a < b < c < d

\(\left\{\begin{matrix}a\le x\\b\le x\\c\ge x\\d\ge x\end{matrix}\right.;a< b< c< d}\)

Đúng(0)

LD

Lê Duy Tâm

24 tháng 1 2018 - olm

Tìm x thuộc Z biết

a)(x+5).(x-4)>0

b)(x-3).(x+7)<0

c)(x+3).(x²+1)>0

d)(x²-4).(x²-16)<0

#Hỏi cộng đồng OLM #Toán lớp 6

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP