Tính tổng: B = 3 0 + 3 1 + 3 2 + ... + 3 30
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
26 tháng 6 2019
Đúng(0)
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
21 tháng 7 2023
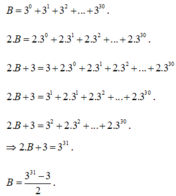
Lời giải:
\(B=\frac{5}{3}+\frac{5}{3^2}+\frac{5}{3^3}+...+\frac{5}{3^{30}}=5(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{30}})\)
\(3B=5(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{29}})\)
\(3B-B=5(1-\frac{1}{3^{30}})=\frac{5(3^{30}-1)}{3^{30}}\)
\(\Rightarrow B=\frac{5(3^{30}-1)}{2.3^{30}}\)
NP
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 9 2023
A = 1 + (1 + 2) + (1 + 2 + 3) + (1 + 2 + 3 + 4)+...+ (1 + 2 + 3+...+ 30)
A = 1 + (2+1)\(\times\)2: 2+ (3+1)\(\times\)3: 2 + ....+ (30 +1) \(\times\) 30: 2
A = 1 + 2 \(\times\)3: 2 + 3 \(\times\) 4 : 2 +...+ 30 \(\times\) 31:2
A = \(\dfrac{2+2\times3+3\times4+...+30\times31}{2}\)
Đặt B = 2 + 2 \(\times\) 3 + 3 \(\times\) 4 +...+ 30 \(\times\) 31
1 x 2 x 3 = 1 x 2 x3 = 1 x 2 x 3
2 x 3 x 3 = 2 x 3 x ( 4 - 1) = 2 x 3 x 4 - 1 x 2 x 3
3 x 4 x 3 = 3 x 4 x (5- 2) = 3 x 4 x 5 - 2 x 3 x 4
...........................................................................
30 x 31 x 3 = 30 x 31 x (32 - 29) = 30 x 31 x 32 - 29 x 31 x 30
Cộng vế với vế ta có:
B x 3 = 30 x 31 x 32 ⇒ B = 30 x 31 x 32 : 3 = 14880
A = B : 2 = 14880 : 2 = 7440
12 tháng 10 2021
So sánh:
a) 5^300 và 3^500
b) (-16)^11 và (-32)^9
c) (2^2)^3 và 2^2^3
d) 2^30 + 2^30 + 4^30 và 3^20 + 6^20 + 8^20
e) 4^30 và 3×24^10
g) 2^0 + 2^1 + 2^2 + 2^3 +...+ 2^50 và 2^51
BT
1
AH
Akai Haruma
Giáo viên
30 tháng 3 2023
Bạn nên viết đề bằng công thức toán để được hỗ trợ tốt hơn.
NT
4
XO
3 tháng 10 2019
A = 1 + 32 + 34 + 36 + ... + 328 + 330
=> 32A = 32 + 34 + 36 + 38 + ... + 330 + 332
Lấy 32A trừ A theo vế ta có :
32A - A = (32 + 34 + 36 + 38 + ... + 330 + 332) - (1 + 32 + 34 + 36 + ... + 328 + 330)
9A - A = 332 - 1
8A = 332 - 1
A \(\frac{3^{32}-1}{8}\)
TD
1
AH
Akai Haruma
Giáo viên
30 tháng 6
Lời giải:
$A=(-3)^0+(-3)^1+(-3)^2+...+(-3)^{2012}$
$(-3)A=(-3)^1+(-3)^2+(-3)^3+...+(-3)^{2013}$
$\Rightarrow (-3)A-A=(-3)^{2013}-(-3)^0$
$\Rightarrow -4A=-3^{2013}-1$
$\Rightarrow A=\frac{-3^{2013}-1}{-4}=\frac{3^{2013}+1}{4}$