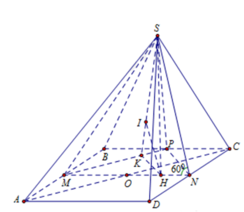
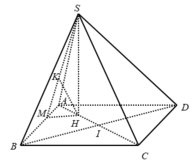
Cho hình chóp có đáy là hình vuông tâm O, cạnh bằng 4a. Cạnh bên SA = 2a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng là trung điểm của H của đoạn thẳng AO. Tính khoảng cách d giữa các đường thẳng SD và AB.
A. d = 4a.
B. d = 4 a 22 11
C. d = 2a
D. d = 3 a 2 11

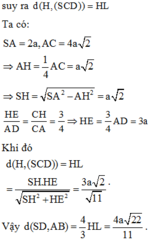


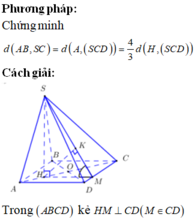
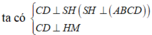
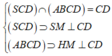
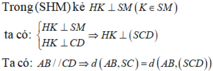
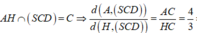

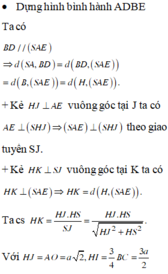
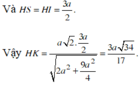
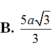
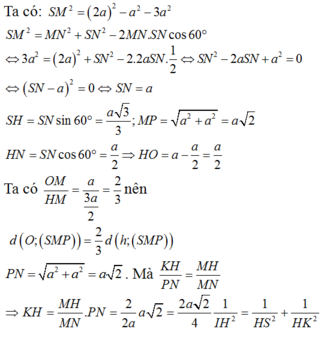
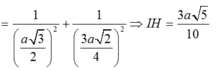




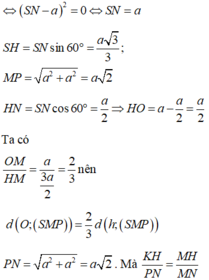
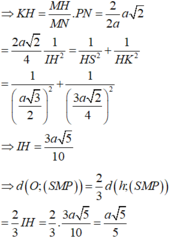

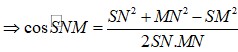
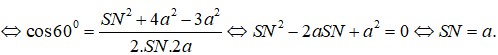

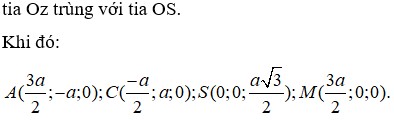
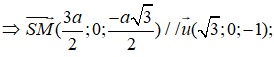
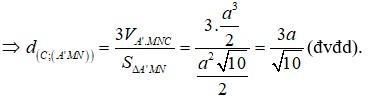

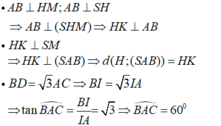
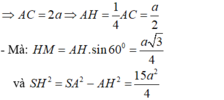
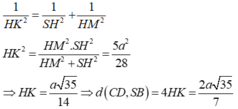
Phương pháp:
Sử dụng lí thuyết d(a,b) = d(a,(P)) = d(A,(P)), ở đó a,b chéo nhau, (P) chứa b và song song a và A ∈ a để tìm khoảng cách giữa hai đường thẳng SD, AB.
Tính khoảng cách và kết luận.
Cách giải:
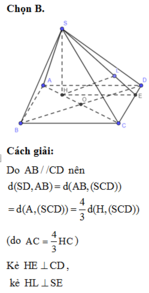
Do AB//CD nên
Kẻ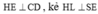
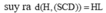
Ta có: SA = 2a,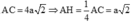
Khi đó