Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = AB = a, AD = 2a. Tính khoảng cách h từ A tới mặt phẳng (B’D’C)
A. h = a
B. h = 2 a 3
C. h = 3 a 2
D. h = 4 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

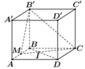
Khoảng cách từ D đến (B'MC)
gấp hai lần khoảng cách từ B đến (B'MC)

Đáp án B
Ta có d D ; A B ' C = d B ; A B ' C mà A M A D = 3 4
Và 1 d 2 B ; A B ' C = 1 A B 2 + 1 B C 2 + 1 B B ' ⇒ d M ; A B ' C = a 2 .
Gọi E, F lần lượt là trung điểm của AD’, B’C.
Suy ra EF là đoạn vuông góc chung cuả AD’, B’C.
Do đó d A D ' ; B ' C = E F = A B = a . Vậy x y = a . a 2 = a 2 2 .

Chọn D.
Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.

ta có :
\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)
Mà BB'=A'A=a
\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)
=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)
=> dM,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\) (2)
tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)
và \(AB=a\sqrt{2}\)
=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\) (3)
Từ (1), (2)&(3)
=> dM;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)
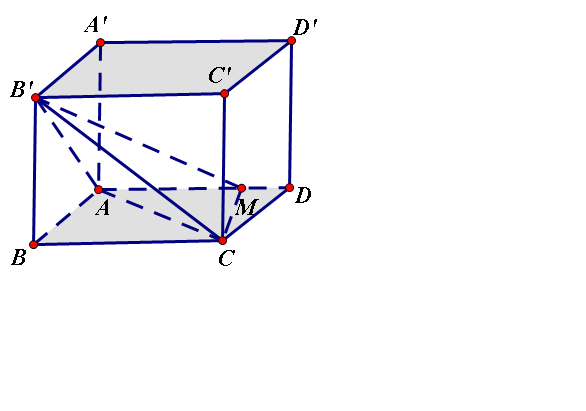
Pytago tính đuợc 3 cạnh
, \(MC=\frac{a\sqrt{5}}{2}\)
Dùng công thức Heron =>\(S_{AMC}=\frac{3a^2}{4}\)
\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)
Mặt khác dùng công thức Heron cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)
=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)
Đáp án D
Gọi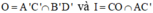 thì IA = 2IC’ = 2h có
thì IA = 2IC’ = 2h có