Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là các tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, C và tiêp xúc với đường thẳng AD tại A. Bán kính R của mặt cầu (S) bằng
A. R = a 6
B. R = a 6 3
C. R = a 6 5
D. R = a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B

Gọi K là trọng tâm tam giác ABC, N đỗi xứng với D qua J, qua K kẻ KO song song với DN ta có O là tâm mặt cầu cần xác định.
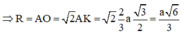

Gọi E là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}AE\perp BC\\DE\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ADE\right)\)
Trong tam giác cân ADE (cân tại E), kẻ \(DH\perp AE\Rightarrow DH\perp\left(ABC\right)\)
\(\Rightarrow\widehat{DAE}=45^0\Rightarrow\Delta ADE\) vuông cân tại E
Gọi G và G' lần lượt là trọng tâm ABC và BCD. Trong mp (ADE), qua G kẻ đường thẳng d song song DE, qua G' kẻ d' song song AE. Gọi O là giao điểm d và d' \(\Rightarrow\) O là tâm mặt cầu ngoại tiếp tứ diện
Ta có: \(AE=DE=\dfrac{a\sqrt{3}}{2}\) ; \(AG=\dfrac{2}{3}AE=\dfrac{a\sqrt{3}}{3}\) ; \(OG=OG'=\dfrac{1}{3}AE=\dfrac{a\sqrt{3}}{6}\)
\(R=OA=\sqrt{AG^2+OG^2}=\dfrac{a\sqrt{15}}{6}\)

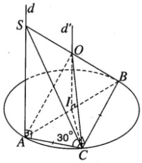
Trường hợp mặt phẳng (SBC) tạo với mặt phẳng (ABC) một góc 30 ° thì góc của hai mặt phẳng đó chính là góc ∠ SCA. Thực vậy vì SA ⊥ (ABC) mà AC ⊥ CB nên ta có SC ⊥ CB. Do đó ∠SCA = 30 ° .
Vì AB = 2a nên ta có AC = a 2 ta suy ra
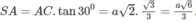
Gọi r là bán kính mặt cầu ngoại tiếp tứ diện khi ∠ SCA = 30 °
Ta có r = SB/2 = OA = OB = OC = OS, trong đó SB 2 = SA 2 + AB 2
Vậy
![]()
Do đó 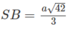
Ta suy ra 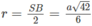

Đáp án C
Ta có A D 2 = A B 2 + B D 2 = A C 2 + C D 2
⇒ Δ A B D , Δ A C D vuông cân tại B, C
Mà O là trung điểm cạnh A D ⇒ O A = O B − O C
⇒ O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Dễ thấy O A = O B − O C và Δ A B C đều cạnh a
⇒ khối chóp O . A B C là hình chóp tam giác đều

Cho mặt cầu (S) có bán kính bằng 5. Xét khối tứ diện ABCD có các đỉnh đều thuộc mặt cầu (S) và tam giác ABC vuông cân tại B, DA = DB = DC. Thể tích khối tứ diện ABCD lớn nhất bằng a/b. Với a,b là các số nguyên dương và phân số a/b tối giản. Tính a + b.
A. 1173
B. 4081
C. 128
D. 5035
Cho mặt cầu (S) có bán kính bằng 5. Xét khối tứ diện ABCD có các đỉnh đều thuộc mặt cầu (S) và tam giác ABC vuông cân tại B, DA = DB = DC. Thể tích khối tứ diện ABCD lớn nhất bằng a/b. Với a,b là các số nguyên dương và phân số a/b tối giản. Tính a + b.
A. 1173
B. 4081
C. 128
D. 5035
Chọn đáp án B