Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ bên. Đặt g x = f f x . Tìm số nghiệm của phương trình g ' x = 0 .

A. 2
B. 4
C. 6
D. 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Ta có ![]() ∀
x
∈
R
∀
x
∈
R
Khi đó ![]()
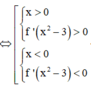
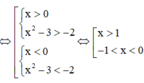
Suy ra hàm số đồng biến trên khoảng (–1;0) và (1;+ ∞)
Đáp án D.
Kí hiệu trên đồ thị như hình bên.
Đặt u = f x . Ta có g x = f f x = f u .
g ' x = u ' . f ' u = f ' x . f ' u
g ' x = 0 ⇔ f ' x = 0 f ' u = 0
f ' x = 0 ⇔ x 1 = 0 x 2 = a 2 < a < 3 (nhìn hình để xác định a).
f ' u = 0 ⇔ u = x 1 u = x 2 ⇔ f x = x 1 = 0 f x = x 2 = a 2 < a < 3
f x = 0 ⇔ x ∈ b ; 1 ; c = x 3 ; x 4 ; x 5
f x = a (nhìn vào đồ thị thể hiện bên ta thấy đồ thị hàm số f x cắt đường thẳng y = a (với 2 < a < 3 ) tại ba điểm phân biệt do vậy phương trình f x = a có ba nghiệm phân biệt x 6 ; x 7 ; x 8 .
Rõ ràng x 1 ,..., x 8 là đôi một khác nhau.
Kết hợp lại thì phương trình g ' x = 0 có 8 nghiệm phân biệt.