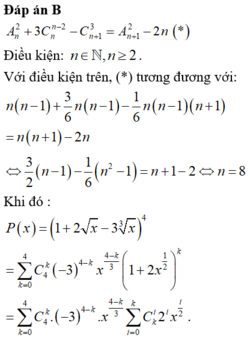Cho khai triển . Tìm hệ số lớn nhất trong khai triển trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

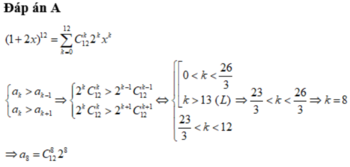

Xét khai triển: \(\left(x+1\right)^n\) với \(n\ge5\)
SHTQ: \(C_n^k.x^k\)
Số hạng chứa \(x^5\Rightarrow k=5\) có hệ số \(C_n^5\)
Hệ số của \(x^5\) trong khai triển đã cho:
\(C_6^5+C_7^5+C_8^5+...+C_{12}^5=...\)

Chọn B
Ta có a8= C88+C98+C108+C118+C128= 1+9+45+165+495= 715

A n 2 + 3 C n n - 2 - C n + 1 3 = A n + 1 2 - 2 n
Điều kiện: n ∈ ℕ , n ≥ 2
Với điều kiện trên, (*) tương đương với:
n n - 1 + 3 6 n n - 1 - 1 6 n n - 1 n + 1 = n n - 1 - 2 n
⇔ 3 2 n - 1 - 1 6 n 2 - 1 = n + 1 - 2 ⇔ n = 8
Khi đó :
P x = 1 + 2 x - 3 x 3 4 = ∑ k = 0 4 C 4 k - 3 4 - k x 4 - k 3 1 + 2 x 1 2 k = ∑ k = 0 4 C 4 k - 3 4 - k x 4 - k 3 . ∑ C k i i = 0 k . 2 i x i 2
Hệ số của số hạng x ứng với
4 - k 3 + i 2 = 1 ⇔ 2 k = 3 i = 2
Vì i , k ∈ ℕ và i ≤ k ≤ 4 nên ta suy ra: k = 4, i = 2 hoặc k = 2 và i = 4.Như vậy hệ số của x trong khai triển là:
C 4 - 4 - 3 0 . C 4 2 . 2 2 + C 4 2 - 3 2 . C 2 0 . 2 0 = 78
Đáp án cần chọn là B

a) \(|x+7|+|2y-12|=0\)
Vì \(\hept{\begin{cases}|x+7|\ge0;\forall x,y\\|2y-12|\ge0;\forall x,y\end{cases}}\)\(\Rightarrow|x+7|+|2y-12|\ge0;\forall x,y\)
Do đó \(|x+7|+|2y-12|=0\)
\(\Leftrightarrow\hept{\begin{cases}|x+7|=0\\|2y-12|=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-7\\y=6\end{cases}}\)
Vậy ...
các phần sau tương tự
a) Ta có :
\(\left|x+7\right|\ge0\)
\(\left|2y-12\right|\ge0\)
Để |x+7| + | 2y - 12| = 0
=> x +7 = 0 và 2y - 12= 0
x = 7 2y = 12
y = 12 : 2
y = 6
Vậy x = 7 ; y = 6

Xét khai triển : (x + 1)n
Tk+1 = \(C_n^k\). xk . 110 - k = \(C_n^k\) . xk.
+) Cụ thể với khai triển (x + 1)10. Số hạng chứa x8 ứng với k = 8
Số hạng x8 trong khai triển này là \(C_{10}^8\) . x8 = 45x8
+) Cụ thể với khai triển (x + 1)11. Số hạng chứa x8 ứng với k = 8
Số hạng x8 trong khai triển này là \(C_{11}^8\) . x8 = 165x8
+) Cụ thể với khai triển (x + 1)12. Số hạng chứa x8 ứng với k = 8
Số hạng x8 trong khai triển này là \(C_{12}^8\) . x8 = 495x8
Vậy hệ số của x8 trong khai triển của đa thức trên là : 165 + 495 + 45 = 705