Cho phân thức
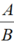
viết phân thức nghịch đảo của nó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Với \(\dfrac{A}{B}\ne0\)
\(\Rightarrow\) Phân thức nghịch đảo là: \(\dfrac{B}{A}\)

Phân thức nghịch đảo của \(\dfrac{x-1}{x+2}\) là \(\dfrac{x+2}{x-1}\)

Hướng dẫn:
+ Phân thức nghịch đảo của phân thức (x + 1)/(x - 2) là (x - 2)/(x + 1).
+ Phân thức nghịch đảo của phân thức (2x)/1 là 1/(2x).
+ Phân thức nghịch đảo của phân thức x - 1 là 1/(x - 1).

a. Gọi phân số cần tìm là \(\frac{a}{b}\)
\(\Rightarrow\) Phân số nghịch đảo là \(\frac{b}{a}\)
Theo bài ra, ta có:
\(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow\frac{a^2+b^2}{ab}\ge2\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow a^2-ab+b^2-ab\ge0\)
\(\Leftrightarrow a\left(a-b\right)+b\left(b-a\right)\ge0\)
\(\Leftrightarrow a\left(a-b\right)-b\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)
Vì (a-b)2 chắc chắn lớn hơn hoặc bằng 0
\(\Rightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Vậy tổng của một phân số dương với ghịch đảo của nó luôn lớn hơn hoặc bằng 2.