Cho hàm số f x liên tục trên ℝ và f x + 2 f 1 x = 3 x . Tính tích phân I = ∫ 1 2 2 f x x d x
A. I = 1 2
B. I = 5 2
C. I = 3 2
D. I = 7 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 9 2018
Chọn đáp án C.
Lấy tích phân hai vế trên đoạn [0;2] có
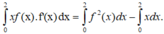
Tích phân từng phần có
CM
21 tháng 3 2019
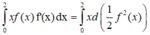
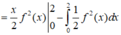
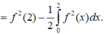
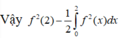
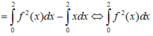
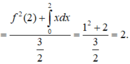
Đáp án A
Đặt t = x ⇔ d t = d x 2 x ⇔ d x = 2 d t ; x = 0 ⇒ t = 0 x = 4 ⇒ t = 2
Khi đó I = ∫ 0 4 f ' x d x = ∫ 0 2 2 t . f ' t d t = 2 ∫ 0 2 t . f ' t d t
Đặt u = t d v = f ' t d t ⇔ d u = d t v = f t ⇒ 2 ∫ 0 2 t . f ' t d t = t . f t 0 2 - ∫ 0 2 f t d t = 2 f 2 - 1 = - 5
Vậy tích phân I = 2 . - 5 = - 10 .
CM
23 tháng 1 2019
• Xét 
Đặt 
suy ra 2tdt = dx
Đổi cận 
Suy ra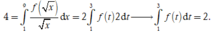 
• Xét 
Đặt u = sin x , suy ra du = cosxdx
Đổi cận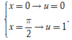 
Suy ra 
Vậy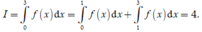 
Chọn C.
CM
7 tháng 2 2017
Đáp án C
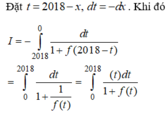
Do đó 2 I = I + I = ∫ 0 2018 1 1 + f ( x ) d x + ∫ 0 2018 f ( x ) 1 + f ( x ) d x = ∫ 0 2018 1 d x = 2018
Vậy I = 1019
CM
10 tháng 5 2018
Đáp án C.
Ta có f 2 - f 1 = ∫ 1 2 f ' x d x ≥ ∫ 1 2 x + 1 x d x = x 2 2 + ln x 1 2 = 2 + ln 2 - 1 2 = 3 2 + ln 2 .
Mặt khác f 1 = 1 suy ra f 2 ≥ f 1 + 3 2 + ln 2 = 1 + 3 2 + ln 2 = 5 2 + ln 2 .
Đáp án C
Ta có I = ∫ 1 2 2 f x x d x = I = ∫ 1 2 2 1 x 3 x − 2 f 1 x d x = 3 ∫ 1 2 2 d x − 2 ∫ 1 2 2 1 x f 1 x d x
Đặt t = 1 x ⇔ d t = − d x x 2 ⇔ d x = − d t t 2 và x = 1 2 ⇒ t = 2 x = 2 ⇒ t = 1 2 .
Suy ra ∫ 1 2 2 1 x f 1 x d x = ∫ 1 2 2 f t t d t
Vậy I = 3 ∫ 1 2 2 d x − 2 ∫ 1 2 2 f t t d t = 9 2 − 2 ∫ 1 2 2 f t t d t ⇒ 3 I = 9 2 ⇔ I = 3 2