Tìm các số nguyên x, y biết: (x + l)3 = -125;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
29 tháng 6
2/
$n\vdots 65, n\vdots 125$
$\Rightarrow n=BC(65,125)$
$\Rightarrow n\vdots BCNN(65,125)$
$\Rightarrow n\vdots 1625$
$\Rightarrow n=1625k$ với $k$ tự nhiên.
$n=1625k=5^3.13.k$
Nếu $k=1$ thì $n$ có $(3+1)(1+1)=8$ ước (loại)
Nếu $k>1$ thì $n$ có ít nhất $(3+1)(1+1)(1+1)=16$ ước nguyên tố.
$n$ có đúng 16 ước nguyên tố khi mà $k$ là 1 số nguyên tố.
Vậy $n=1625p$ với $p$ là số nguyên tố.
5 tháng 3 2019
a) 135x4y chia hết cho 45
Ta có: 135x4y chia hết cho 5 và 9
Để 135x4y chia hết cho 5 => y = 0 hoặc 5
135x4y chia hết cho 9 => (1 + 3 + 5 + x + 4 + y) chia hết cho 9
=> (13 + x + y) chia hết cho 9
Nếu: y = 0 thì x = 5 => 135540
y = 5 thì x = 0 => 135045
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
\(x^6+\left(y^6+15y^4+75y^2+125\right)+z^3-3x^2y^2z-15x^2z=0\)
\(\Leftrightarrow x^6+\left(y^2+5\right)^3+z^3=3x^2\left(y^2+5\right)z\)
Ta có:
\(x^6+\left(y^2+5\right)^3+z^3\ge3\sqrt[3]{x^6\left(y^2+5\right)^3z^3}=3x^2\left(y^2+5\right)z\)
Đẳng thức xảy ra khi và chỉ khi:
\(x^2=y^2+5=z\)
Từ \(x^2=y^2+5\Rightarrow\left(x-y\right)\left(x+y\right)=5\)
\(\Rightarrow\left(x;y\right)=\left(3;2\right)\Rightarrow z=9\)
Vậy có đúng 1 bộ số nguyên dương thỏa mãn pt:
\(\left(x;y;z\right)=\left(3;2;9\right)\)
O
1
DA
29 tháng 3 2020
/ x - 1 /. / y + 1 / = 2
Vì x,y là các số nguyên nên ta xét các trường hợp sau :
TH1 : x = 1 ; y = 2
=> / x - 1 /. / y + 1 / = 0 ( Loại )
TH2 : x = 2 ; y = 1
=>/ x - 1 /. / y + 1 / = 2 ( T/mãn )
TH3 : x = -1 ; y = -2
=>/ x - 1 /. / y + 1 / = 2 ( T/mãn )
TH4 : x = -2 ; y = -1
=>/ x - 1 /. / y + 1 / = 0 ( Loại )
Vậy \(\left(x,y\right)\in\left[\left(2,1\right);\left(-1,-2\right)\right]\)
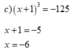
Từ đề bài ta có x = 1 = -5, tìm được x = -6