Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
)
:
x
-
1
2
+
y
-
2
2
+
z
-
2
2
=
9
và hai điểm M(4;-4;2), N(6;0;6). Gọi E là điểm thuộc mặt cầu (S) sao cho EM+EN đạt giá trị lớn nhất. Viết phương trình tiếp diện của mặt cầu (S) tại E. A. x-2y+2z +8=0 B. 2x+y-2z-9=0 C. 2x+2y+z+1=0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S ) : x - 1 2 + y - 2 2 + z - 2 2 = 9 và hai điểm M(4;-4;2), N(6;0;6). Gọi E là điểm thuộc mặt cầu (S) sao cho EM+EN đạt giá trị lớn nhất. Viết phương trình tiếp diện của mặt cầu (S) tại E.
A. x-2y+2z +8=0
B. 2x+y-2z-9=0
C. 2x+2y+z+1=0
D. 2x-2y+z+9=0
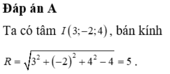
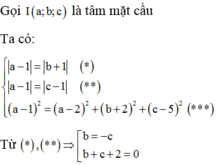
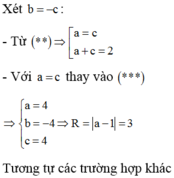
Đáp án D.
Phương pháp giải: Dựng hình, áp dụng công thức trung tuyến để biện luận giá trị lớn nhất
Lời giải:
Xét mặt cầu ( S ) : x - 1 2 + y - 2 2 + z - 2 2 = 9 có tâm I(1;2;2) và bán kính R= 3
=> M, N nằm bên ngoài khối cầu (S).
Gọi H là trung điểm của MN
Lại có
Khi và chỉ khi E là giao điểm của IH và mặt cầu (S).
Gọi (P) là mặt phẳng tiếp diện của (S) tại E
Dựa vào các đáp án ta thấy ở đáp án D,
Vậy phương trình mặt phẳng cần tìm là 2x-2y+z+9=0