Hai điện tích
q
1
=
10
-
6
C
và
q
2
=
4
.
10
-
6
C
đặt cố định trong không khí tại hai điểm A và B...
Đọc tiếp
Hai điện tích q 1 = 10 - 6 C và q 2 = 4 . 10 - 6 C đặt cố định trong không khí tại hai điểm A và B cách nhau một khoảng a = 30cm. Để hệ cân bằng thì phải đặt một điện tích q 0 ở:
A. trong đoạn AB, cách A l0cm
B. trong đoạn AB, cách B l0cm
C. ngoài đoạn AB, cách A l0cm
D. ngoài đoạn AB, cách B l0cm
Đáp án A
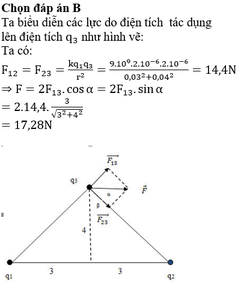
Gọi F 1 → , F 2 → là lực tĩnh điện do q 1 . q 2 tác dụng lên q 0 đặt tại C. Để q 0 nằm cân bằng thì:
F → = F 1 → + F 2 → = 0 → ⇒ F 1 → = - F 2 →
Do đó:
+ q 0 nằm trong đoạn AB (Đặt AC = x; CB = a – x)
+
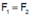hay 
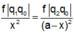(với mọi
q
0
)
Hay