Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm . Trên các cạnh AB, AC, AD lần lượt lấy các điểm sao cho và tứ diện có thể tích nhỏ nhất. Phương trình măt phẳng là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Trên cạnh AB, AC , AD của tứ diện ABCD lần lượt có các điểm B', C', D'. Áp dụng công thức tỷ số thể tích ta có
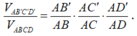
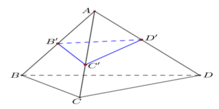
Từ giả thiết
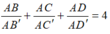
áp dụng bất đẳng thức AM- GM ta có
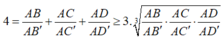
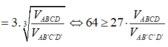
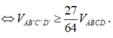
Do thể tích ABCD cố định nên thể tích AB'C'D' nhỏ nhất
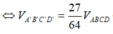
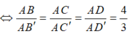
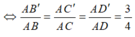
=> (B'C'D') song song với (BCD) và đi qua điểm B'
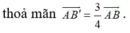
![]()
![]()
suy ra vectơ pháp tuyến của mặt phẳng (B'C'D') là:
![]()
![]()
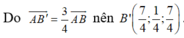
Vậy phương trình (B'C'D') là:
![]()

Đáp án là C.
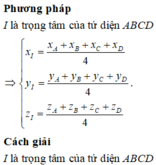
Toạ độ trọng tâm của tứ diện A B C D :
x = x A + x B + x C + x D 4 = 2 y = y A + y B + y C + y D 4 = 3 z = z A + z B + z C + z D 4 = 1


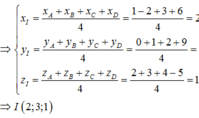
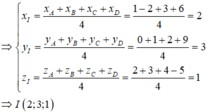
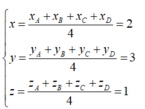


Chọn đáp án C
Áp dụng công thức tỉ số thể tích ta có:
Suy ra thể tích tứ diện AB'C'D' nhỏ nhất khi
Khi đó A B ' ⇀ = 3 4 A B ⇀ và B ' C ' D ' / / B C D
⇒ Mặt phẳng B ' C ' D ' có một vec-tơ pháp tuyến là
Lại có
Phương trình mặt phẳng B ' C ' D '