Question

[Pham Trong Bach]

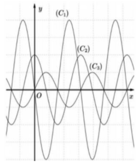
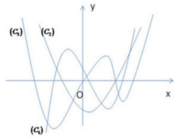
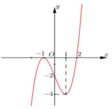
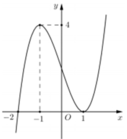
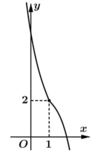
Cho hàm số \ y = f x có đạo hàm trên ℝ . Đường cong trong hình vẽ bên là đồ thị của hàm số y = f ' x ( y = f ' x  liên tục trên ℝ  ). Xét hàm số g x = f x 2 − 2 Mệnh đề nào dưới đây sai ?

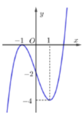
A. Hàm số g x , nghịch biến trên − ∞ ; − 2

B. Hàm số  g x , đồng biến trên  2 ; + ∞

C. Hàm số  g x , nghịch biến trên − 1 ; 0

D. Hàm số , nghịch biến trên 0 ; 2

Answer 1

[Cao Minh Tâm]

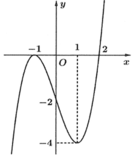
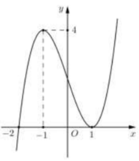
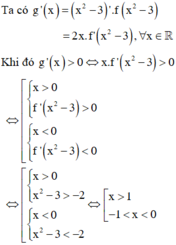
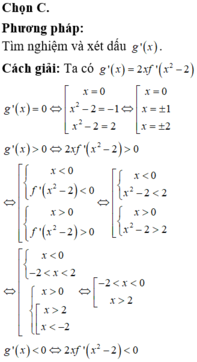
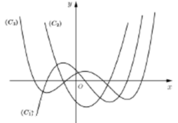
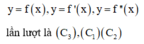
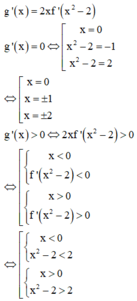
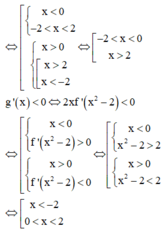
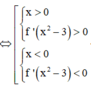
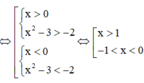
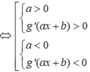
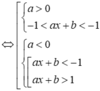
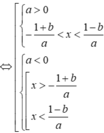
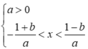
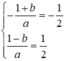
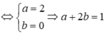
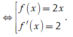
Đáp án C

Xét hàm số g x = f x 2 − 2  trên ℝ ,

có  g ' x = x 2 − 2 ' . f ' x 2 − 2 = 2 x . f ' x 2 − 2

Phương trình

  g ' x = 0 ⇔ x . f ' x 2 − 2 = 0 ⇔ x = 0 f ' x 2 − 2 = 0 ⇔ x = 0 x 2 − 2 = − 1 x 2 − 2 = 2 ⇔ x = 0 x = ± 1 x = ± 2

Với \ x > 2 ⇔ x 2 − 2 > 0  mà f ' x > 0 , ∀ x ∈ 2 ; + ∞  

suy ra  f ' x 2 − 2 > 0 , ∀ x ∈ 2 ; + ∞

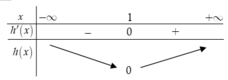
Bảng biến thiên

x	-∞          -2            -1             0               1               2     +∞
f ' x 2 − 2	+       0     -      0      -     0      -      0      -     0        +
g x	-             +               +              -              -               +