Cho hàm số
f
x
=
x
2
x
khi
x
<
1,
x
≠
0
0
khi
x
=
0
x
khi
x
≥
1
. Chọn khẳng định đúng A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn
0
;
1
B. Hàm số liên tục tại mọi điểm trừ điểm x=0 C. Hàm số liên tục tại mọi điểm thuộc...
Đọc tiếp
Cho hàm số f x = x 2 x khi x < 1, x ≠ 0 0 khi x = 0 x khi x ≥ 1 . Chọn khẳng định đúng
A. Hàm số liên tục tại mọi điểm trừ các điểm thuộc đoạn 0 ; 1
B. Hàm số liên tục tại mọi điểm trừ điểm x=0
C. Hàm số liên tục tại mọi điểm thuộc R
D. Hàm số liên tục tại mọi điểm trừ điểm x=1
ta cần phải nhớ.
xác định trên khoảng 
và 
được gọi là liên tục tại 
nếu 
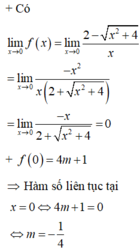
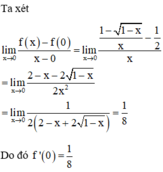
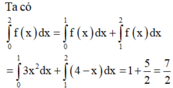
Đáp án C.
Tập xác định: D = ℝ .
Nếu x ≠ 0, x ≠ 1 thì hàm số y = f x liên tục trên mỗi khoảng − ∞ ; 0 , 0 ; 1 và 1 ; + ∞ .
Nếu x = 0 thì f 0 = 0 và lim x → 0 − f x = lim x → 0 − x 2 x = lim x → 0 − x = 0 lim x → 0 + f x = lim x → 0 + x 2 x = lim x → 0 + x = 0
Suy ra f 0 = lim x → 0 − f x = lim x → 0 + f x = lim x → 0 f x = 0 và hàm số y = f x liên tục tại điểm x=0.
Nếu x = 1 thì f 1 = 1 = 1 và lim x → 1 − f x = lim x → 1 − x 2 x = lim x → 1 − x = 1 lim x → 1 + f x = lim x → 1 + x = 1
Suy ra f 1 = lim x → 1 − f x = lim x → 1 + f x = lim x → 1 f x = 1 và hàm số y = f x liên tục tại điểm x=1.
Vậy hàm số y = f x liên tục trên R .