Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y = x - m 2 - 2 x - m trên đoạn [0;4] bằng -1.
A. 0
B. 2
C. 3
D. 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 9 2019
Đáp án C
Xét hàm số f x = x 2 − 2 x + m trên đoạn [-1;2]
Tạ có: f ' x = 2 x − 2 = 0 ⇒ x = 1
Lại có: f 0 = m ; f − 1 = m − 1 ; f 2 = m + 2
Do đó f x ∈ m − 1 ; m + 2
Nếu m − 1 ≥ 0 ⇒ max 0 ; 2 f x = m + 2 = 5 ⇔ m = 3
Nếu m − 1 < 0 suy ra max 0 ; 2 f x = m + 2 max 0 ; 2 f x = 1 − m
TH1: max 0 ; 2 f x = m + 2 = 5 ⇔ m = 3 k o _ t / m
TH2: max 0 ; 2 f x = 1 − m ⇔ m = − 4 ⇒ m + 1 = − 3 t / m
Vậy m = 3 ; m = − 4 là giá trị cần tìm
Chọn D
Điều kiện: x ≠ m
Hàm số đã cho xác định trên [0;4] khi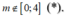
Ta có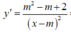
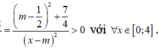
Hàm số đồng biến trên đoạn [0;4] nên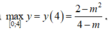
Kết hợp với điều kiện (*) ta được m = -3. Do đó có một giá trị của m thỏa yêu cầu bài toán.