Gọi S là tập hợp các giá trị của m để hàm số y = | x 3 - 3 x 2 + m | đạt giá trị lớn nhất bằng 50 trên [-2;4]. Tổng các phần tử thuộc S là
A. 4
B. 36
C. 140
D. 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 3 2017
Chọn D
Xét hàm số y =
x
2
-
m
x
+
2
m
x
-
2
trên [-1;1] có: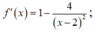 
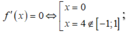
Bảng biến thiên
Trường hợp 1. 
Khi đó
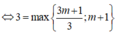
Trường hợp 2. 
Khả năng 1.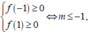 
Khi đó 
Khả năng 2 
Khi đó 
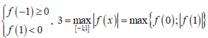
Trường hợp này vô nghiệm.
Khả năng 3. 
Khi đó 
Vô nghiệm.
Vậy có hai giá trị thỏa mãn là 
Do đó tổng tất cả các phần tử của S là -1.
CM
15 tháng 12 2019
+ Xét hàm số f(x) = x3-3x+ m là hàm số liên tục trên đoạn [0; 2] .
Ta có đạo hàm f’ (x) = 3x2- 3 và f’ (x) = 0 khi x= 1 ( nhận ) hoặc x= -1( loại)
+ Suy ra GTLN và GTNN của f(x) thuộc { f(0); f(1) ; f(2) }={m;m-2; m+2}.
+ Xét hàm số y = x 3 - 3 x + m trên đoạn [0; 2 ] ta được giá trị lớn nhất của y là
m a x m ; m - 2 ; m + 1 = 3 .
TH1: m= 3 thì max {1;3;5}= 5 ( loại )
TH2: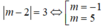 
+ Với m= -1. Ta có max {1; 3}= 3 (nhận).
+Với m= 5. Ta có max { 3;5;7}= 7 (loại).
TH3: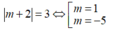 
+ Với m= 1. Ta có max {1; 3}= 3 (nhận).
+ Với m= -5. Ta có max {3;5;7}= 7 (loại).
Do đó m= -1 hoặc m= 1
Vậy tập hợp S có phần tử.
Chọn B.
CM
12 tháng 12 2018
Đáp án B.
Xét f x = x 3 − 3 x + m trên đoạn 0 ; 2
Ta có: f ' x = 3 x 3 3 = 0 ⇒ x = 1
Lại có:
f 0 = m ; f 1 = m − 2 ; f 2 = m + 2
Do đó: f x ∈ m − 2 ; m + 2
Nếu
m − 2 ≥ 0 ⇒ Max 0 ; 2 f x = m + 2 = 3 ⇔ m = 1 (loại).
Nếu m − 2 < 0 ⇒ Max 0 ; 2 f x = m + 2 Max 0 ; 2 f x = 2 − m
TH1: Max 0 ; 2 f x = m + 2 = 3 ⇔ m = 1 ⇒ 2 − m = 1 < 3 t / m
TH2: Max 0 ; 2 f x = 2 − m = 3 ⇔ m = − 1 ⇒ m + 2 = 1 < 3 t / m
Vậy m = 1 ; m = − 1 là giá trị cần tìm.
Chọn A
Xét hàm số g(x) = x 3 - 3 x 2 + m có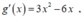
Xét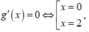 
Khi đó giá trị lớn nhất của hàm số y = | x 3 - 3 x 2 + m | trên [-2;4] là:
Trường hợp 1: Giả sử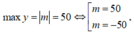
Với m = 50 thì |m + 16| = 66 > 50 (loại)
Với m = -50 thì |m - 20| = 70 > 50 (loại)
Trường hợp 2: Giả sử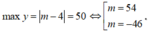
Với m = 54 => |m| = 54 > 50 (loại)
Với m = -46 thì |m - 20| = 66 > 50 (loại)
Trường hợp 3: Giả sử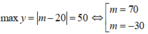
Với m = 70 thì |m + 16| = 86 > 50 (loại)
Với m = -30 thì |m + 16| = 14 < 50,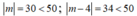
(thỏa mãn)
Trường hợp 4: Giả sử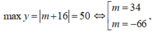
Với m = 34 thì |m| = 34 < 50,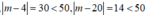
(thỏa mãn)
Với m = -66 thì |m| = 66 > 50 (loại)
Vậy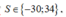
Do đó tổng các phẩn tử của S là: -30 + 34 = 4.