Có bao nhiêu giá trị nguyên của tham số m để hàm số y = m x 4 + m 2 + 1 x 2 + 1 có đúng một điểm cực đại và không có điểm cực tiểu?
A. 1
B. 2
C. 7
D. 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Tập xác định D = ℝ
Trường hợp 1: m − 1 = 0 ⇔ m = 1 , ta có y = 8 x 2 + 1 có đồ thị là parabol, bề lõm quay lên trên nên hàm số chỉ có 1 điểm cực tiểu và không có cực đại
Trường hợp 2: m − 1 ≠ 0 ⇔ m ≠ 1 , vì hàm số trùng phương nên để hàm số chỉ có điểm cực tiểu mà không có cực đại thì a = m − 1 > 0 a b = 2 m − 1 m + 3 ≥ 0 ⇔ − 3 ≤ m < 1
Do đó không có m nguyên dương thỏa mãn trong trường hợp này
Kết luận: vậy m = 1 thì hàm số y = 1 − m x 4 + 2 m + 3 x 2 + 1 có đúng một điểm cực tiểu và không có điểm cực đại

Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn

+ Đạo hàm y’ = -3x2+ 6x+ 3( m2-1) = -3( x2- 2x-m2+1).
Đặt g( x) = x2- 2x-m2+1 là tam thức bậc hai có ∆ ' = m 2 .
+ Do đó hàm số đã cho có cực đại cực tiểu khi và chỉ khi y’ =0 có hai nghiệm phân biệt hay g(x) =0 có hai nghiệm phân biệt
⇔ ∆ ' > 0 ⇔ m ≠ 0 . (1)
+ Khi đó y’ có các nghiệm là: 1±m .
Tọa độ các điểm cực trị của đồ thị hàm số là A( 1-m ; -2-2m3) và B( 1+m ; -2+ 2m3).
Ta có:
O A → ( 1 - m ; - 2 - 2 m 3 ) ⇒ O A 2 = ( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 . O B → ( 1 + m ; - 2 + 2 m 3 ) ⇒ O B 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 .
Để A và B cách đều gốc tọa độ khi và chỉ khi OA= O B hay OA2= OB2
( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 ⇔ - 4 m + 16 m 3 = 0
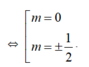
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.
Vậy không có giá trị nguyên nào của m thỏa mãn yêu cầu bài toán.
Chọn A.

Đáp án C
TH1: ![]() suy ra
suy ra ![]() hàm số có
hàm số có ![]() điểm cực đại
điểm cực đại ![]() nhận m=0.
nhận m=0.
TH2: ![]() .
.
Theo yêu cầu bài toán
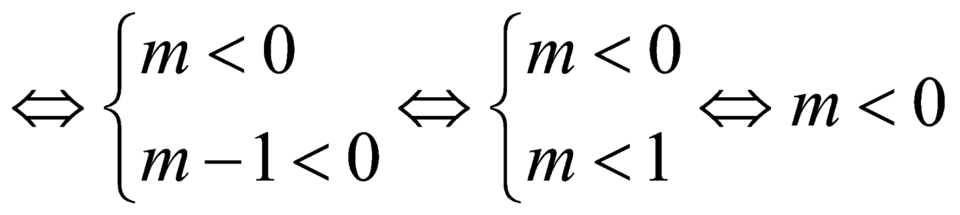 .
.
Vậy ![]() là giá trị cần tìm.
là giá trị cần tìm.
Chọn đáp án B