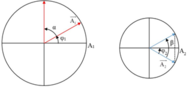
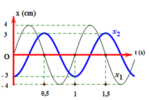
Hai vật tham gia hai dao động điều hoà cùng phương, cùng vị trí cân bằng với li độ x 1 và x 2 có đồ thị như hình vẽ. Khoảng cách giữa hai vật vào thời điểm t = 1,125s là
A. 4,48 cm
B. 5 cm
C. 4,95 cm
D. 3,32 cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
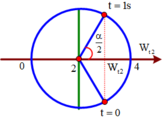
Ta thấy tại t = 0, vật 2 qua vị trí 4 cm theo chiều âm, tại t = 1,75 s thì vật 2 qua VTCB theo chiều dương
suy ra 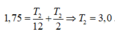
Ta quan sát tại giao điểm cuối cùng của 2 chất điểm trên đồ thị, khi đó chất điểm 1 qua VTCB theo chiều dương còn chất điểm hai qua VTCB theo chiều âm nên
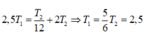 s
s

Chọn A
Ta thấy tại t = 0, vật 2 qua vị trí 4 cm theo chiều âm, tại t = 1,75 s thì vật 2 qua VTCB theo chiều dương
suy ra 1 , 75 = T 2 12 + T 2 2 ⇒ T 2 = 3 , 0 s.
Ta quan sát tại giao điểm cuối cùng của 2 chất điểm trên đồ thị, khi đó chất điểm 1 qua VTCB theo chiều dương còn chất điểm hai qua VTCB theo chiều âm nên 2 , 5 T 1 = T 2 12 + 2 T 2 ⇒ T 1 = 5 6 T 2 = 2 , 5 s.

Đáp án D
Gọi phương trình dao động của 2 vật lần lượt là:
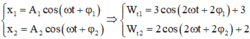
Từ t = 0 đến t = 1 s, hai vật đều quay được cùng góc α như trên đường tròn:
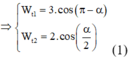
vì
ω
1
=
ω
2
= ω,
m
1
=
m
2
= m →
k
1
=
k
2
= k và 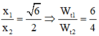 (2)
(2)
Từ (1) và (2), suy ra: 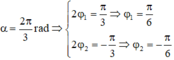 (3)
(3)
Từ t = 0 đến t = 1s hết 1s:
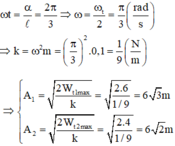 (4)
(4)
Từ (3) và (4), suy ra: 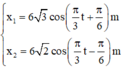 =>
=> 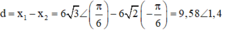
Hay 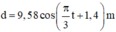
Thay t = 3,69 s vào d ta tìm được khoảng cách giữa 2 vật là: 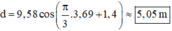

Đáp án D
Phương trình li độ:
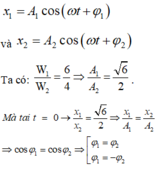
Vì quan sát đồ thị ta thấy hai đồ thị dao động không đồng biến nên hai dao động này không phải cùng pha nhau nên loại trường hợp ![]()
Trong 1 s ban đầu, vật một từ vị trí ban đầu đến vị trí có thế năng bằng 0 (x1 = 0), vật hai từ vị trí ban đầu đến vị trí có cùng thế năng.
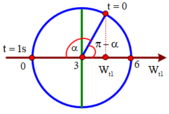
Mặt khác quan sát đồ thị, tại t = 0, Wt1 giảm (x1 giảm) và Wt2 tăng (x2 tăng)→ ta biểu diễn trên VTLG (như hình).
Tại t = 1 s, vật 2 quay trở về vị trí ban đầu lần đầu tiên nên vecto ![]() đối xứng qua trục hoành
đối xứng qua trục hoành ![]()
Vì hai vật cùng tần số nên trong 1 giây ban đầu góc quay α = β.
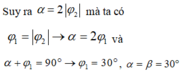
Góc quay α = ωt = π/3 → T = 6 s và vật một dao động sớm pha π/3 so với vật hai.
Biên độ dao động:

Khoảng cách giữa hai vật
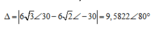
Suy ra tại t = 3,69 s thì ∆ ≈ 5 m