Bất phương trình nào sau đây không tương đương với bất phương trình x 5 ≥ 0 ? A. x - 1 2 x 5 ≥ 0 B. -...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

PT

Pham Trong Bach

24 tháng 12 2017

Bất phương trình nào sau đây không tương đương với bất phương trình x + 5 ≥ 0 ? A. x - 1 2 x + 5 ≥ 0 B. - x 2 x + 5 ≤ 0 C. x + 5 x + 5 ≥ 0 D. x + 5 x - 5 ≥ 0 ...

1

CM

Cao Minh Tâm

24 tháng 12 2017

Đáp án D

Những câu hỏi liên quan

PT

Pham Trong Bach

6 tháng 12 2019

Bất phương trình nào sau đây không tương đương với bất phương trình x + 5 ≥ 0 ? ...

#Toán lớp 12

1

CM

Cao Minh Tâm

6 tháng 12 2019

PT

Pham Trong Bach

15 tháng 3 2017

Bất phương trình nào sau đây không tương đương với bất phương trình x + 5 ≥ 0?

A. (x - 1 ) 2 (x + 5) ≥ 0

B. - x 2 (x + 5) ≤ 0

C. x + 5 (x + 5) ≥ 0

D. x + 5 (x - 5) ≥ 0

#Toán lớp 10

1

CM

Cao Minh Tâm

15 tháng 3 2017

Chọn D.

+) Xét bất phương trình x + 5 ≥ 0 ⇔ x ≥ -5

⇒ Tập nghiệm của bất phương trình là S = [-5;+ ∞ )

+) Xét bất phương trình (x - 1 ) 2 (x + 5) ≥ 0

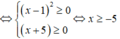
Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 1)

Tập nghiệm của bất phương trình là S = [-5; + ∞ ).

+) Xét bất phương trình - x 2 (x + 5) ≤ 0

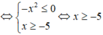
Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 1)

Tập nghiệm của bất phương trình là S = [-5; + ∞ ).

+) Xét bất phương trình

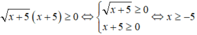
Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 1)

Tập nghiệm của bất phương trình là S = [-5; + ∞ ).

+) Xét bất phương trình

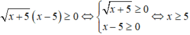
Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 1)

Tập nghiệm của bất phương trình là S = [5; + ∞ ).

Vậy bất phương trình

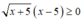
Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 1)

không tương đương với bất phương trình x + 5 ≥ 0.

PT

Pham Trong Bach

29 tháng 8 2017

Bất phương trình nào sau đây tương đương với bất phương trình x + 5 ≥ 0?

A. - x 2 ( x + 5 ) ≥ 0

B. ( x - 1 ) 2 ( x + 5 ) ≥ 0

C. x - 1 ( x + 5 ) ≥ 0

D. ( x + 5 ) 2 ≥ 0

#Toán lớp 10

1

CM

Cao Minh Tâm

29 tháng 8 2017

Đáp án B.

Ta thấy bất phương trình ở đề bài và bất phương trình (x - 1 ) 2 (x + 5) ≥ 0 cùng có tập nghiệm là: [-5; + ∞ ). Do đó, hai bất phương trình này tương đương với nhau

NH

Nguyễn Hữu Tuyết Hạnh

13 tháng 4 2020 - olm

5A. Các cặp bất phương trình sau đây có tương đương không?a) x≤3 và 2x≤6 b) x2 + 3 >0 và |3x+1| < -15B. bất phương trình sau đây có tương đương không? Vì saOa) 2+x >4 và -x < -2 b) ( x2+1 )x ≥ 0 và 2x4 ≥ 06A. Cho hai bất phương trình x+5 ≥ |m2+2m| + 12 và x≥7 . Tìm m để hai bất phương trình tương đương.6B. Tìm các giá trị của m để hai bất phương trình x< -2 và x< \(\frac{m^2+4m-9}{2}\) tương...

0

PT

Pham Trong Bach

24 tháng 9 2017

Bất phương trình 3x - 2(y - x + 1) > 0 tương đương với bất phương trình nào trong số các bất phương trình sau đây?

A. x - 2y - 2 > 0

B. 5x - 2y - 2 > 0

C. 5x - 2y - 1 > 0

D. 4x - 2y - 2 > 0

#Toán lớp 10

1

CM

Cao Minh Tâm

24 tháng 9 2017

3x - 2(y - x + 1) > 0 ⇔ 3x - 2y + 2x - 2 > 0 ⇔ 5x - 2y - 2 > 0

Đáp án là B.

PT

Pham Trong Bach

12 tháng 1 2019

Với giá trị nào của a thì hai bất phương trình sau đây tương đương? (a-1) x- a+ 3> 0 (1) (a+1) x-a+2> 0 (2) A. a = 1 B. a = 5 C. a = - 1 D. -1 < a <...

#Toán lớp 10

1

CM

Cao Minh Tâm

12 tháng 1 2019

Chọn B

TH1.Nếu a-1=0 hay a =1 thì

(1) thành: 2 > 0 ( luôn đúng mọi x) Tập nghiệm của bất phương trình T = R

(2) thành: 2x+1> 0 hay x> -1/2 Tập nghiệm của bất phương trình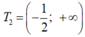

Vậy a= 1 không thỏa yêu cầu bài toán.

TH2. Nếu a+1= 0 hay a= -1thì

(1) thành: -2x=4>0 hay x< 2. Tập nghiệm của bất phương trình T₂ = (-∞; 2)

(2) thành: 3> 0 luôn đúng Tập nghiệm của bất phương trình T= R

Vậy a= -1 không thỏa yêu cầu bài toán.

TH3.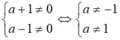

(1) : (a-1) x> a-3 và (2) : (a+1) x> a-2

Hai bất phương trình tương đương

PT

Pham Trong Bach

22 tháng 12 2018

Cho bất phương trình 4 + 1 x - 1 > 2 x - 1 x - 1 ( x ≠ 1 ) . Bất phương trình nào sau đây không tương đương với bất phương trình đã cho? A. 2 > x - 1 x - 1 B. 4 ( x - 1 ) + 1 x - 1 > 2 x ( x - 1 ) - 1 x ...

#Toán lớp 10

1

CM

Cao Minh Tâm

22 tháng 12 2018

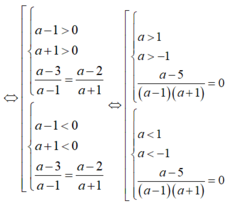
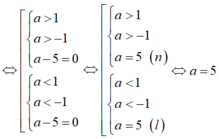
Ta thấy x= 1 không là nghiệm của bất phương trình đã cho nhưng x= 1 là nghiệm của bất phương trình 4(x -1)+ 1> 2x(x-1) – 1.

Do đó, hai bất phương trình này không tương đương với nhau.

Chọn C.

QT

Quoc Tran Anh Le

Giáo viên

26 tháng 9 2023

Các bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Nếu là bất phương trình bậc hai một ẩn, \(x = 2\) có là nghiệm của bất phương trình đó hay không?

a) \({x^2} + x - 6 \le 0\)

b) \(x + 2 > 0\)

c) \( - 6{x^2} - 7x + 5 > 0\)

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

26 tháng 9 2023

a) \({x^2} + x - 6 \le 0\) là một bất phương trình bậc hai một ẩn

Vì \({2^2} + 2 - 6 = 0\) nên \(x = 2\) là nghiệm của bất phương trình trên

b) \(x + 2 > 0\) không là bất phương trình bậc hai một ẩn

c) \( - 6{x^2} - 7x + 5 > 0\) là một bất phương trình bậc hai một ẩn

Vì \( - {6.2^2} - 7.2 + 5 = - 33 < 0\) nên \(x = 2\) không là nghiệm của bất phương trình trên

PT

Pham Trong Bach

20 tháng 3 2018

Các cặp bất phương trình sau đây có tương đương không? Vì sao?

a) x ≥ 0 và x − 3 ≥ − 3 ; b) x < 0 và − x 2 ≤ 0

1

CM

Cao Minh Tâm

20 tháng 3 2018

a) Tương đương b) Không tương đương.