Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA=OB=a,OC=2a. Gọi M là trung điểm cạnh BC. Côsin góc giữa hai đường thẳng AB và OM bằng
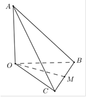
A. 10 10
B. 10 5
C. 3 10 10
D. 15 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt
O
A
=
O
B
=
O
C
= a suy ra ![]()
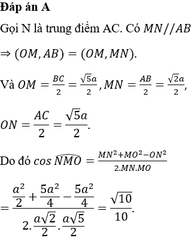
Gọi N là trung điểm AC, ta có MN//AB. Khi đó ![]()
Trong tam giác OMN có ![]() nên OMN là tam giác đều
nên OMN là tam giác đều
![]()
Chọn C.

Gọi N là trung điểm của AC ⇒ M N / / A B , Vậy
( OM,AB ) = ( OM,MN ) = OMN
Cho OA = OB = OC = 1. Ta có.
M N = A B 2 = 2 2 O M = B C 2 = 2 2 O N = A C 2 = 2 2
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Đáp án cần chọn là C

Đáp án C
Cách 1.
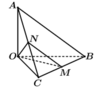
Gọi N là trung điểm của AC ⇒ M N / / A B
![]()
Cho OA =OB =OC =1. Ta có.

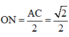
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Cách 2. Dùng pp tọa độ hóa và công thức


Gọi N là trung điểm AC \(\Rightarrow MN||AB\Rightarrow\widehat{OMN}\) là góc giữa OM và AB
Đặt \(OA=a\)
\(AB=\sqrt{OA^2+OB^2}=\sqrt{a^2+k^2a^2}=a\sqrt{k^2+1}\)
\(AC=\sqrt{OA^2+OC^2}=a\sqrt{k^2+1}\)
\(BC=\sqrt{OB^2+OC^2}=a.k\sqrt{2}\)
\(MN=\dfrac{1}{2}AB=\dfrac{a}{2}\sqrt{k^2+1}\) ; \(OM=\dfrac{BC}{2}=a.\dfrac{k\sqrt{2}}{2}\) ; \(ON=\dfrac{1}{2}AC=a.\dfrac{\sqrt{k^2+1}}{2}\)
\(cos\widehat{OMN}=cos60^0=\dfrac{OM^2+MN^2-ON^2}{2OM.MN}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{a^2.\dfrac{k^2}{2}}{2.a^2.\dfrac{k\sqrt{2k^2+2}}{4}}=\dfrac{1}{2}\Leftrightarrow2k=\sqrt{2k^2+2}\)
\(\Leftrightarrow4k^2=2k^2+2\Rightarrow k=1\)

Đáp án C.
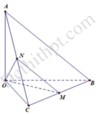
Do OA,OB,OC đội một vuông góc với nhau và O A = O B = O C nên tam giác ABC là tam giác đều. Qua M kẻ đường thẳng song song với AB cắt AC tại N
Ta có M N / / A B ⇒ O M , A B = O M , M N ^ ^
Giả sử O A = O B = O C = a ⇒ A B = B C = C A = a 2
Ta có O M = B C 2 = a 2 2 , O N = A C 2 = a 2 2 , M N = A B 2 = a 2 2
⇒ Δ A B C là tam giác đều ⇒ O M N ^ = 60 0
⇒ O M , M N ^ = 60 0 .