Tìm tất cả các giá trị của a sao cho l i m a . 2 n - 3 a + 2 n + 1 = 1
A. a = 1
B. a = 2
C. a = -3
D. a ≠ 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a) Để B là phân số thì n -3 \(\ne\)0 => n\(\ne\)3
b) Để B có giá trị là số nguyên thì n+4 \(⋮\)n-3
\(\frac{n+4}{n-3}\)= \(\frac{n-3+7}{n-3}\)= \(\frac{7}{n-3}\)Vì n+4 \(⋮\)n-3 nên 7 \(⋮\)n-3
=> n-3 \(\in\)Ư(7) ={ 1;7; -1; -7}
=> n\(\in\){ 4; 10; 2; -4}
Vậy...
c) Bn thay vào r tính ra

a: 12/3n-1 là số nguyên khi 3n-1 thuộc Ư(12)
=>3n-1 thuộc {1;-1;2;-2;3;-3;4;-4;6;-6;12;-12}
mà n là số nguyên
nên n thuộc {0;1;-1}
c: 2n+5/n-3 là số nguyên
=>2n-6+11 chia hết cho n-3
=>n-3 thuộc {1;-1;11;-11}
=>n thuộc {4;2;14;-8}

\(a,ĐK:x\ge1;x\ne3\\ b,A=\dfrac{\left(\sqrt{x-1}+\sqrt{2}\right)\left(\sqrt{x-1}-\sqrt{2}\right)}{\sqrt{x-1}-\sqrt{2}}=\sqrt{x-1}+\sqrt{2}\)

1) Tìm tập hợp A sao cho các số nguyên a sao cho:
=> \(\dfrac{1}{2}\) +\(\dfrac{1}{34}\) \(\le\) \(\dfrac{a}{17}\) <\(\dfrac{15}{17}\) - \(\dfrac{3}{17}\)
\(\dfrac{17}{34}\)+\(\dfrac{1}{34}\)\(\le\)\(\dfrac{a}{34}\)<\(\dfrac{12}{17}\)
\(\dfrac{18}{34}\) \(\le\)\(\dfrac{a}{34}\)<\(\dfrac{24}{34}\)
=> a \(\in\) {18; 19; 20; 21; 22; 23 }
2)
Để A là số nguyên thì 2 phải chia hết cho n-1
=> n-1 \(\in\) ước của 2
=> n-1\(\in\) {1;-1;2;-2}
=> n\(\in\) {-1; 0; 2; 3}

Để A nhận giá trị nguyên thì 2n+1n+22n+1n+2 nguyên
⇔2n+1⋮n+2⇔2n+1⋮n+2
⇒(2n+4)−4+1⋮n+2⇒(2n+4)−4+1⋮n+2
⇒2(n+2)−3⋮n+2⇒2(n+2)−3⋮n+2
2(n+2)⋮n+22(n+2)⋮n+2
⇒−3⋮n+2⇒−3⋮n+2
⇒n+2∈Ư(−3)⇒n+2∈Ư(−3)
⇒n+2∈{−1;−3;1;3}⇒n+2∈{−1;−3;1;3}
⇒n∈{−3;−5;−1;1}

a, Tập hợp con của A là{1} ,{2}, A,∅
b, Để M ⊂A và M⊂B
thì M={1}
c,Vì A⊂N và B⊂N
Nên N={1;2;4}

Ta có
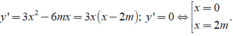
Hàm số có hai điểm cực trị khi y’= 0 có hai nghiệm phân biệt suy ra
0≠2m hay m≠0
Tọa độ các điểm cực trị của đồ thị hàm số là: A( 0; 2) và B( 2m; 2-4m3).
Suy ra ![]()
Theo giả thiết A; Bvà M thẳng hàng 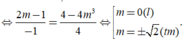
Chọn D.
Đáp án B
Ta có l i m a . 2 n - 3 a + 2 n + 1 = l i m a . 2 n - 3 a + 2 . 2 n = l i m a - 3 2 n 2 + a 2 n = a 2 = 1 ⇒ a = 2