Cho hình hộp chữ nhật ABCD A'B'C'D' có khoảng cách giữa hai đường thẳng AB và B'C bằng khoảng cách giữa hai đường thẳng BC và AB' và bằng
2
a
5
5
. Khoảng cách giữa hai đường thẳng AC và BD' là
a
3
3
. Tính thể tích V của khối hộp chữ nhật đã cho A.
V
=
a
3
B.
V
=
8
a
3
C.
V
=
2
a
3
D.
...
Đọc tiếp
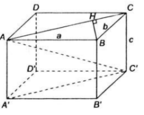
Cho hình hộp chữ nhật ABCD A'B'C'D' có khoảng cách giữa hai đường thẳng AB và B'C bằng khoảng cách giữa hai đường thẳng BC và AB' và bằng 2 a 5 5 . Khoảng cách giữa hai đường thẳng AC và BD' là a 3 3 . Tính thể tích V của khối hộp chữ nhật đã cho
A. V = a 3
B. V = 8 a 3
C. V = 2 a 3
D. V = 3 a 3
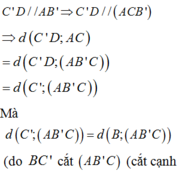
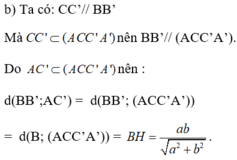
Đáp án C.
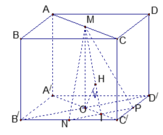
Giả sử các kích thước của hình hộp chữ nhật là A B = x , A D = y , A A ' = z . Trong đó x , y , z > 0 . Để giải bài toán, ta phân tích từng dữ kiện có trong đề bài.
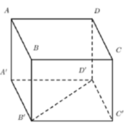
1. Khoảng cách giữa hai đường thẳng AB và B'C bằng 2 a 5 5 .
Ta có
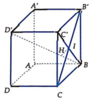
A B / / C D C D ⊂ A ' B ' C D A B ⊄ A ' B ' C D ⇒ A B / / A ' B ' C D ⇒ d A B ; B ' C = d A B ; A ' B ' C D
= d A ; A ' B ' C D = A H = 2 a 5 5 với H là hình chiếu của A trên .
Từ 1 A H 2 = 1 A A ' 2 + 1 A D 2 ⇒ 1 y 2 + 1 z 2 = 5 4 a 2 (1)
2. Khoảng cách giữa hai đường thẳng BC và AB' bằng 2 a 5 5 .
Tương tự, ta chứng minh được
B C / / A B ' C ' D ⇒ d B C ; A B ' = d B C ; A B ' C ' D
= B K = 2 a 5 5
với K là hình chiếu của B trên AB'.
Từ 1 B K 2 = 1 B A 2 + 1 B B ' 2 ⇒ 1 x 2 + 1 z 2 = 5 4 a 2 (2)
3. Khoảng cách giữa hai đường thẳng AC và BD' là a 3 3 .
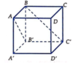
Gọi O = A C ∩ B D ⇒ O là trung điểm của BD. Gọi I là trung điểm của DD' thì OI là đường trung bình của Δ B D D ' ⇒ O I / / B D ' ⇒ B D ' / / A C I
⇒ d B D ' ; A C = d B D ' ; A C I = d D ' ; A C I = d D ; A C I
Ta thấy DI, DA, DC đôi một vuông góc với nhau nên:
1 d 2 D ; A C I = 1 D A 2 + 1 D C 2 + 1 D I 2 = 1 D A 2 + 1 D C 2 + 4 D D ' ⇒ 1 x 2 + 1 y 2 + 4 z 2 = 3 a 2
(3)
Giải hệ phương trình gồm (1), (2) và (3) ta tìm được: x = y = z , z = 2 a .
Vậy thể tích của khối hộp chữ nhật đã cho là V = x y z = a . a .2 a = 2 a 3 (đvtt).