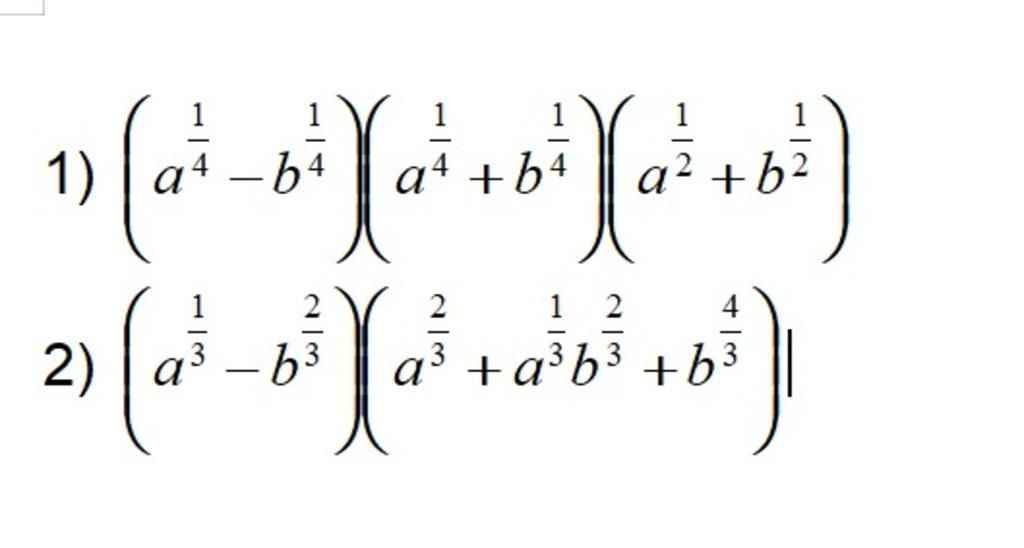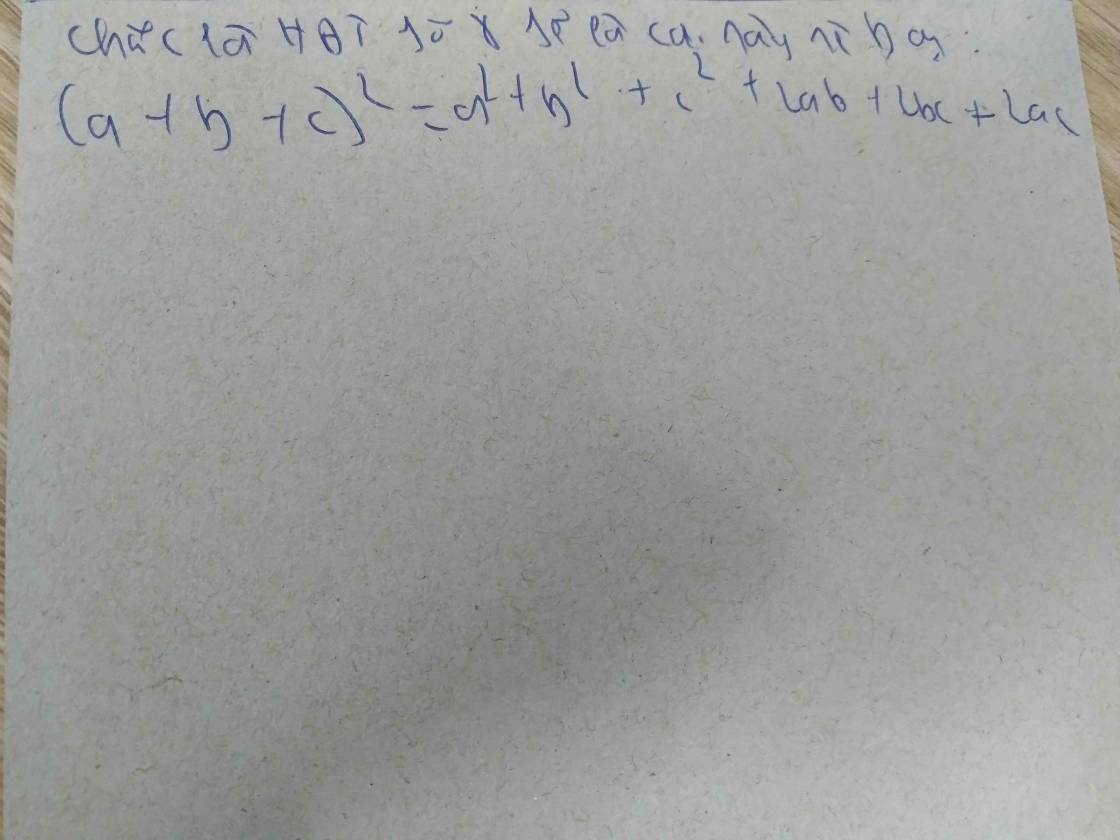n^2 có phải hằng đẳng thức?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2
18 tháng 11 2023
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`
NH
3
23 tháng 9 2020
\(4x^2-4\)
\(=4\left(x^2-1\right)\)
\(=4\left(x-1\right)\left(x+1\right)\)
TN
2
KD
9 tháng 10 2020
\(25x^2-2=0\)
\(\left(5x\right)^2-\left(\sqrt{2}\right)^2=0\)
Bây giờ mình đã phân tích ra HĐT số 3 rồi nên bạn có thể tự làm!
31 tháng 7 2019
Biểu thức trên ko thể biến đổi ngược thành hằng đẳng thức nhé bạn
Muốn trở thành hằng đẳng thức, có 2 cách
C1: Hằng đẳng thức tổng hai lập phương
\(\left(x+4\right)\left(x^2-4x+16\right)=x^3+64\)
C2: Hằng đẳng thức hiệu hai lập phương
\(\left(x-4\right)\left(x^2+4x+16\right)=x^3-64\)
PM
1
MN
29 tháng 1 2020
Ta có :
\(x^3-3x^2-3x+1=0\)
\(\Leftrightarrow x^3+x^2-4x^2-4x+x+1=0\)
\(\Leftrightarrow x^2\left(x+1\right)-4x\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-4x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x^2-4x+1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-1\\\left(x-2\right)^2-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=2\pm\sqrt{3}\end{cases}}\)
Vậy tập nghiệm của phương trình là : \(S=\left\{-1;2+\sqrt{3};2-\sqrt{3}\right\}\)