Cho các số thực a, b khác 0. Xét hàm số f x = a x + 1 3 + b x e x với ∀ x ≠ − 1. Biết f ' 0 = − 22 và ∫ 0 1 f x d x = 5. Tính a + b
A. 19
B. 7
C. 8
D. 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Ta có
f ' x = - 3 a x + 1 4 + b e x + b x e x
nên f’(0) = x – 3a + b = –22 (1).
Xét
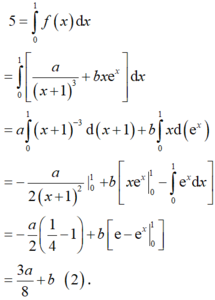
Từ (1) và (2) ta có
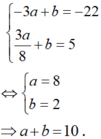

a: f(-2)=4+3=7
f(-1)=2+3=5
f(0)=3
f(1/2)=-1+3=2
f(-1/2)=1+3=4
b: g(-1)=1-1=0
f(0)=0-1=-1

Đáp án D
Ta có ∫ 0 1 f x d x = ∫ 0 1 a x + 1 3 d x + ∫ 0 1 b x e x d x = − a 2 1 x + 1 2 0 1 + ∫ 0 1 b x e x d x = 3 a 8 + ∫ 0 1 b x e x d x .
Đặt u = x d v = e x ⇒ d u = d x v = e x ⇒ ∫ 0 1 b x e x d x = b x e x − 0 1 ∫ 0 1 b e x d x = b x e x 0 1 − b e x 0 1 = b .
Suy ra ∫ 0 1 f x d x = 3 a 8 + b = 5 1 .
Mặt khác f ' x = − 3 a x + 1 4 + b e x + b x e x ⇒ f ' 0 = − 3 a + b = − 22 2
Từ (1) và (2) suy ra a = 8 ; b = 2 ⇒ a + b = 10.
Đáp án A
Ta có:
∫ 0 1 f x d x = ∫ 0 1 a x + 1 3 d x + ∫ 0 1 b x e x d x = − a 2 1 x + 1 2 0 1 + ∫ 0 1 b x e x d x = 3 a 8 + ∫ 0 1 b x e x d x
Đặt:
u = x d v = e x d x ⇒ d u = d x v = e x ⇒ ∫ 0 1 b x e x d x = b x e x 0 1 − ∫ 0 1 b e x d x = b x e x 0 1 − b e x 0 1 = b
Suy ra ∫ 0 1 f x d x = 3 a 8 + b = 5 1
Mặt khác f ' x = − 3 a x + 1 4 + b e x + b x e x ⇒ f ' 0 = − 3 a + b = − 22 2
Từ 1 , 2 suy ra a = 8 ; b = 2 ⇒ a + b = 10