Cho hàm số y = f x liên tục và không âm trên R thỏa mãn f x . f ' x = 2 x f 2 x + 1 và f 0 = 0 . Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f x trên đoạn 1 ; 3 . Biết rằng giá trị của biểu thức P = 2 M − m có dạng a 11 − b 3 + c , a , b , c ∈ ℤ . Tính a + b + c
A. a + b + c = 4
B. a + b + c = 7
C. a + b + c = 6
D. a + b + c = 5


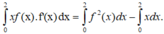
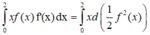
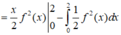
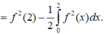
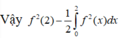
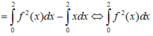
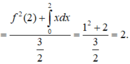



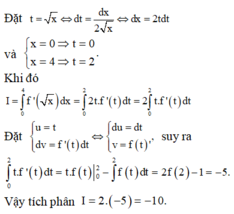
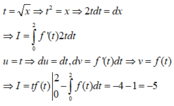

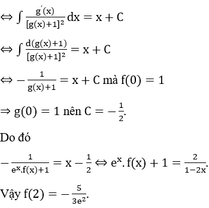
Đáp án B.
Từ
f x . f ' x = 2 x f 2 x + 1 ⇒ f x . f ' x f 2 x + 1 = 2 x ⇒ ∫ f x . f ' x f 2 x + 1 d x = ∫ 2 x d x
(1)
Đặt
f 2 x + 1 = t ⇒ f 2 x = t 2 − 1 ⇒ 2 f x . f ' x d x = 2 t d t ⇒ f x . f ' x d x = t d t
Suy ra ∫ f x . f ' x f 2 x + 1 x = ∫ t d t t = ∫ d t = t + C 1 = f 2 x + 1 + C 1 và ∫ 2 x d x = x 2 + C 2
Từ (1) ta suy ra f 2 x + 1 + C 1 = x 2 + C 2 . Do f 0 = 0 nên C 2 − C 1 = 1 .
Như vậy
f 2 x + 1 = x 2 + C 2 − C 1 = x 2 + 1 ⇒ f 2 x = x 2 + 1 2 − 1 = x 4 + 2 x 2
⇒ f x = x 4 + 2 x 2 = x x 2 + 2 = x x 2 + 2
(do x ∈ 1 ; 3 ).
Ta có f ' x = x 2 + 2 + x 2 x 2 + 2 = 2 x 2 + 1 x 2 + 2 > 0, ∀ x ∈ ℝ ⇒ Hàm số f x = x x 2 + 2 đồng biến trên R nên f x cũng đồng biến trên 1 ; 3 .
Khi đó M = max 1 ; 3 f x = f 3 = 3 11 và m = min 1 ; 3 f x = f 1 = 3 .
Vậy
P = 2 M − m = 6 11 − 3 ⇒ a = 6 ; b = 1 ; c = 0 ⇒ a + b + c = 7