Một chiếc thuyền xuôi dòng sông từ A đến B hết 2 giờ 30 phút. Khi quay ngược dòng từ B đến A mất 3 giờ. Vận tốc của nước so với bờ sông và vận tốc của thuyền so với nước là không đổi. Tính thời gian để chiếc thuyền không nổ máy tự trôi từ A đến B là bao nhiêu?.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VT
Vũ Thành Nam
19 tháng 4 2018
Đúng(0)
Những câu hỏi liên quan
VT
3 tháng 6 2018
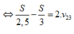
Chọn D
+ Gọi v 13 là vận tốc của thuyền với bờ
v 23 là vận tốc của nước với bờ bằng
v 12 là vận tốc của thuyền so với dòng nước
+ Khi xuôi dòng: v 13 = v 12 + v 23
+ Khi ngược dòng: v 13 = v 12 - v 23 ⇒ v 13 - v 13 = 2 v 23
⇔ S 2 , 5 - S 3 = 2 . v 23 ⇒ v 23 = 1 2 ( S 2 , 5 - S 3 ) ⇒ t c = S v 23 = 30 h
N
21 tháng 10 2021
\(2\left(\dfrac{m}{s}\right)=7,2\left(\dfrac{km}{h}\right)\)
Ta có:
+ Thời gian xuôi dòng:
\(t_{xd}=\dfrac{AB}{v_{tn}+v_{nb}}=1\Rightarrow AB=v_{tn}+v_{nb}\left(1\right)\)
+ Thời gian ngược dòng:
\(t_{nd}=\dfrac{AB}{v_{tn}-v_{nb}}=3\Rightarrow AB=3v_{tn}-3v_{nb}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow v_{tn}=14,4\left(\dfrac{km}{h}\right)=4\left(\dfrac{m}{s}\right)\)
15 tháng 5 2016
Gọi x(km/h) là vận tốc thực của thuyền máy
ĐK:x\(\ge\)2
Vận tốc lúc xuôi dòng: x+2 km/h
Vận tốc lúc ngược dòng: x-2 km/h
Thời gian lúc xuôi dòng từ A đến B: \(\frac{42}{x+2}\) h
Thời gian lúc ngược dòng từ B về A: \(\frac{42}{x-2}\) h
Vì thời gian lúc ngược dòng nhiều hơn thời gian xuôi dòng là 1 h 12' =\(\frac{6}{5}\)h nên ta có phương trình:
\(\frac{42}{x-2}-\frac{42}{x+2}=\frac{6}{5}\)
=>6x2-864=0
Giải phương trình ta được: x1=12(nhận) ; x2=-12(loại)
Vậy vận tốc xuôi dòng là 14 km/h vận tốc ngược dòng là 10 km/h
14 tháng 5 2018
Vận tốc xuôi dòng là:
45,2 + 4,4 = 49,6 km/h
Vận tốc ngược dòng là:
45,2 - 4,4 = 40,8 km/h
Đổi: 2 giờ 30 phút = 2,5 giờ
Quãng đường AB là:
49,6 x 2,5 = 124 km
Thời gian đi ngược dòng của thuyền máy là:
124 : 40,8 = 3,03 giờ = 3 giờ 2 phút
14 tháng 8 2016
a) gọi van toc cano la v ta co;
30: (v-5) = 1h30p = 3/2
v = 25km/h
b) thoi gian cano di xuoi la;
30:(v+5) = 30/25+5 = 30/30 = 1h