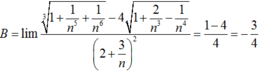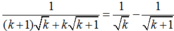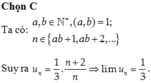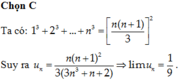Tính giới hạn của dãy số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

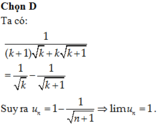

Một câu thôi: Liên hợp
\(\dfrac{1}{2\sqrt{1}+\sqrt{2}}=\dfrac{2.1-\sqrt{2}}{2^2-2}=\dfrac{2-\sqrt{2}}{2}=1-\dfrac{1}{\sqrt{2}}\)
\(\dfrac{1}{3\sqrt{2}+2\sqrt{3}}=\dfrac{3\sqrt{2}-2\sqrt{3}}{9.2-4.3}=\dfrac{3\sqrt{2}-2\sqrt{3}}{6}=\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}\)
\(\Rightarrow\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\)
Nên chứng minh bằng quy nạp mạnh cho chặt chẽ, giờ tui buồn ngủ quá nên bạn tự chứng minh nha :(
\(\Rightarrow u_n=1-\dfrac{1}{\sqrt{n+1}}=\dfrac{\sqrt{n+1}-1}{\sqrt{n+1}}\Rightarrow\lim\limits\left(u_n\right)=\lim\limits\dfrac{\sqrt{\dfrac{n}{n}+\dfrac{1}{n}}-\dfrac{1}{\sqrt{n}}}{\sqrt{\dfrac{n}{n}+\dfrac{1}{n}}}=1\)

1/ \(\lim\limits\dfrac{\dfrac{2^n}{7^n}-5.7.\left(\dfrac{7}{7}\right)^n}{\dfrac{2^n}{7^n}+\left(\dfrac{7}{7}\right)^n}=-35\)
2/ \(\lim\limits\dfrac{\dfrac{3^n}{7^n}-2.5.\left(\dfrac{5}{7}\right)^n}{\dfrac{2^n}{7^n}+\dfrac{7^n}{7^n}}=0\)
3/ \(\lim\limits\sqrt[3]{\dfrac{\dfrac{5}{n}-\dfrac{8n}{n}}{\dfrac{n}{n}+\dfrac{3}{n}}}=\sqrt[3]{-8}=-2\)

Nếu ở hệ số ở mũ 2 là 1 có khi xài đạo hàm chút là ra tổng quát, còn cái này thì...khó :D
Gọi q là k đi, máy tui kẹt chữ q, xài On-screen keyboard mệt lắm
\(u_n=k+2k^2+3k^3+...+nk^n\)
Nhận thấy nếu giờ chia k cho un thì sẽ có \(1+2k+3k+...+nk^{n-1}\), ta đã đưa về dạng tổng quát có thể đạo hàm được, sau đó chỉ cần nhân k là ra un
\(\dfrac{u_n}{k}=1+2k+3k^2+...+nk^{n-1}\)
\(f\left(x\right)=1+k+k^2+...+k^n\)
\(\left\{{}\begin{matrix}u_1=1\\q=k\end{matrix}\right.\Rightarrow f\left(x\right)=1.\dfrac{q^{n+1}-1}{q-1}=\dfrac{k^{n+1}-1}{k-1}\)
Dao ham 2 ve:
\(\Rightarrow f'\left(x\right)=1+2k+3k^2+...+nk^{n-1}=\dfrac{\left(k^{n+1}-1\right)'\left(k-1\right)-\left(k-1\right)'\left(k^{n+1}-1\right)}{\left(k-1\right)^2}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{\left(n+1\right)k^n\left(k-1\right)-k^{n+1}+1}{\left(k-1\right)^2}\)
\(f'\left(x\right)=\dfrac{k^n\left[\left(n+1\right)\left(k-1\right)-k\right]+1}{\left(k-1\right)^2}\)
\(\Rightarrow f'\left(x\right)=\dfrac{u_n}{k}\Rightarrow u_n=f'\left(x\right).k=\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]+k}{\left(k-1\right)^2}\)
\(\Rightarrow lim\left(u_n\right)=lim\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]+k}{\left(k-1\right)^2}=\lim\limits\dfrac{k^{n+1}\left[\left(n+1\right)\left(k-1\right)-k\right]}{\left(k-1\right)^2}+\dfrac{k}{\left(k-1\right)^2}\)
\(\left|k\right|< 1\Rightarrow lim\left(k^{n+1}\right)=0\)
\(\Rightarrow\lim\limits\left(u_n\right)=\dfrac{k}{\left(k-1\right)^2}\)
P/s: Một cách làm rất mới mẻ, có thể tổng quát cho nhiều bài toàn sinh ra từ dãy số vừa rồi :D
Lời giải:
\(u_n=q+2q^2+3q^3+...+nq^n\)
\(qu_n=q^2+2q^3+3a^4+...+nq^{n+1}\)
\(\Rightarrow u_n(1-q)=q+q^2+q^3+...+q^n-nq^{n+1}\)
\(\Leftrightarrow u_n(1-q)=q.\frac{q^n-1}{q-1}-nq^{n+1}\)
\(\Leftrightarrow u_n=q.\frac{1-q^n}{(1-q)^2}+\frac{nq^{n+1}}{q-1}=\frac{q-q^{n+1}}{(1-q)^2}+\frac{nq^{n+1}}{q-1}\)
Vì $|q|< 1$ nên $\lim\limits q^{n+1}=0$ nên $\lim\limits u_n=\frac{q}{(1-q)^2}$

\(A=\lim\dfrac{\sqrt{\dfrac{n\left(n+1\right)}{2}}}{n\left(n+999999\right)}=\lim\dfrac{\sqrt{n^2+n}}{\sqrt{2}\left(n^2+999999n\right)}\)
\(=\lim\dfrac{\sqrt{\dfrac{1}{n^2}+\dfrac{1}{n^3}}}{\sqrt{2}\left(1+\dfrac{999999}{n}\right)}=\dfrac{0}{\sqrt{2}}=0\)