Nghiệm của phương trình lượng giác cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π là
A. 0
B. 3 π 4
C. π 2
D. - π 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
20 tháng 5 2019
Đúng(0)
Những câu hỏi liên quan
CM
8 tháng 7 2017
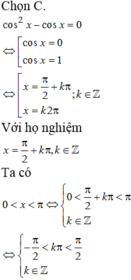
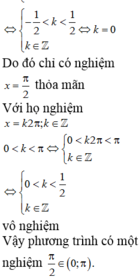
Đáp án A
Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.
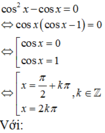
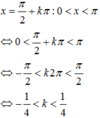
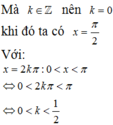
Mà k ∈ ℤ nên không có giá trị k nào thỏa mãn.
Sai lầm và chú ý: Đối với những bài toán giải phương trình lượng giác thỏa mãn điều kiện cho trước, ta cần tìm được x sau đó cho x thỏa mãn điều kiện đầu bài và cô lập được k khi đó ta sẽ tìm được giá trị nguyên k thỏa mãn và sẽ tìm đc x.
CM
29 tháng 9 2017
Đáp án A
Phương pháp: Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.
Cách giải:
cos 2 x − cos x = 0
⇔ cos x cos x − 1 = 0
⇔ cos x = 0 cos x = 1
⇔ x = π 2 + k π x = 2 k π , k ∈ ℤ
+) Với: x = π 2 + k π : 0 < x < π ⇔ 0 < π 2 + k π < π ⇔ − π 2 < k 2 π < π 2 ⇔ − 1 4 < k < 1 4
Mà k ∈ ℤ nên k = 0 khi đó ta có x = π 2
+) Với: x = 2 k π : 0 < x < π ⇔ 0 < 2 k π < π ⇔ 0 < k < 1 2
Mà k ∈ ℤ nên không có giá trị k nào thỏa mãn.
CM
4 tháng 2 2017
Hướng dẫn giải
Chọn B.
Ta có : cos2 x- cosx = 0 ó cosx. ( cosx – 1) = 0
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
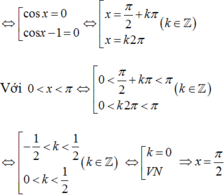
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)