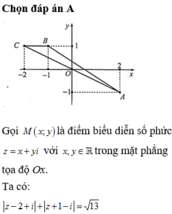
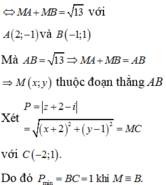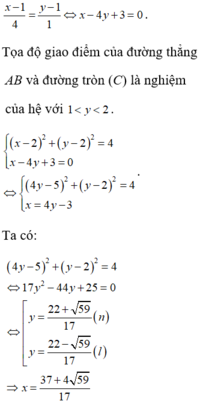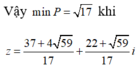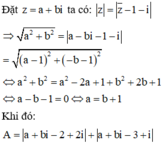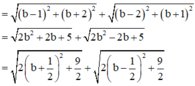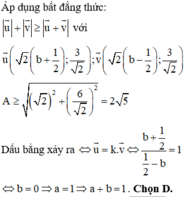Cho số phức z thỏa mãn Giá trị nhỏ nhất của biểu thức là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B.
Đặt ![]() suy ra tập hợp các điểm M(z) = (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R =
5
suy ra tập hợp các điểm M(z) = (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R =
5
Ta có ![]()
![]()
![]()
![]()
![]()
![]()
Ta cần tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung
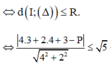
![]()
![]()
Do đó 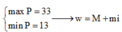
![]()

Chọn đáp án A
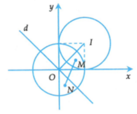

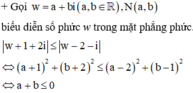
=> Tập hợp các điểm M là nửa mặt phẳng không chứa điểm I(1;1), có bờ là đường thẳng x + y = 0 (d)


Đáp án C
Đặt ![]() Số phức z được biểu diễn bởi điểm N(x;y)
Số phức z được biểu diễn bởi điểm N(x;y)
Số phức ![]() được biểu diễn bởi điểm A(-2;1)
được biểu diễn bởi điểm A(-2;1)
Số phức ![]() được biểu diễn bởi điểm B(5;-6)
được biểu diễn bởi điểm B(5;-6)
được biểu diễn bởi điểm
Ta có: |z + 2 - i| + |z - 5 + 6i| = 7
2
![]() Mà AB = 7
2
nên N thuộc đoạn thẳng AB.
Mà AB = 7
2
nên N thuộc đoạn thẳng AB.
Đường thẳng AB: 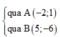
=> phương trình đường thẳng AB là: x + y + 1 = 0
Vì N(x;y) thuộc đoạn thẳng AB nên x + y +1 = 0, x ∈ [-2;5]
Ta có: ![]()
![]()
![]()
![]()
Xét ![]() trên [-2;5] ta có: f'(x) = 4(x-1)
trên [-2;5] ta có: f'(x) = 4(x-1)
![]()
Ta có:
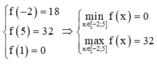
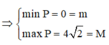
Vậy M + m = 4 2

Đáp án C
Đặt z = x + y i x , y ∈ ℝ ,
khi đó
z − 3 − 2 i ≤ 1 ⇔ x − 3 2 + y − 2 2 ≤ 1
Suy ra tập hợp điểm biểu diễn số phức z là miền trong đường tròn
x − 3 2 + y − 2 2 = 1.
Đặt w = a + b i a , b ∈ ℝ , khi đó w + 1 + 2 i ≤ w − 2 − i ⇔ a + b ≤ 0
Suy ra tập hợp điểm biểu diễn số phức w là miền x + y ≤ 0 , bờ là đường thẳng x + y = 0 .
Gọi C : x − 3 2 + y − 2 2 = 1 có tâm I 3 ; 2 , bán kính R = 1 và Δ : x + y = 0 .
Do đó
P = z − w = M N ⇒ M N min = d I ; Δ − R = 5 2 − 1 = 5 2 − 2 2 .