Từ một tờ giấy hình tròn bán kính R, ta có thể cắt ra một hình chữ nhật có diện tích lớn nhất là bao nhiêu?
A.![]()
B.![]()
C.![]()
D.![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
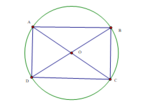
Hình chữ nhật luôn nội tiếp trên một đường tròn, nên hình chữ nhật lớn nhất có thể cắt ra nội tiếp trên đường tròn bán kính 5cm. Xét hình chữ nhật ABCD bất kỳ nội tiếp (0;5cm) ta có
S A B C D = A B . B C ≤ A B 2 + B C 2 2 = A C 2 2 = 10 2 2 = 50 c m 2

Đáp án B
Gọi O là tâm nửa đường tròn. Ta có: P Q = 2 O P = 2 9 − x 2
Đặt diện tích hình chữ nhật là: f x = 2 x 9 − x 2 ⇒ f 2 x = 4 x 2 9 − x 2
Đặt y = x 2 0 < y ≤ 3 . Xét hàm số g y = 4 y 9 − y
Ta có f x lớn nhất khi g y lớn nhất. g y lớn nhất khi y = 3 ⇒ x = 3
max f x = f 3 = 6 2

Đáp án B
Gọi O là tâm nửa đường tròn. Ta có: P Q = 2 O P = 2 9 − x 2
Đặt diện tích hình chữ nhật là: f x = 2 x 9 − x 2 ⇒ f 2 x = 4 x 2 9 − x 2
Đặt y = x 2 0 < y ≤ 3 . Xét hàm số g y = 4 y 9 − y
Ta có f x lớn nhất khi g y lớn nhất. g y lớn nhất khi y = 3 ⇒ x = 3
max f x = f 3 = 6 2

Đáp án C
Ta có x = k . R là chu vi đường tròn đáy của khối nón ⇒ k . R = 2 π r ⇒ r = k . R 2 π
Độ dài đường sinh của khối nón chính là bán kính R ⇒ l = R = r 2 + h 2 ⇒ h = R 2 − r 2
Thể tích của khối nón là:
V = 1 3 π r 2 h = 1 3 π . r 2 . R 2 − r 2 ⇔ V 2 = π 2 9 . r 4 . R 2 − r 2 . 1
Theo bất đẳng thức Cosi, ta được r 2 . R 2 − r 2 = 4. r 2 2 . r 2 2 . R 2 − r 2 ≤ 4 R 6 27 2
Từ (1), (2) suy ra:
V = π 2 9 . 4 R 6 27 = 4 π 2 243 R 6 ⇒ V ≤ 2 π 9 3 R 3
Dấu “=” xảy ra khi:
⇔ r 2 2 = R 2 − r 2 ⇔ R 2 = 3 2 r 2 = 3 2 . k 2 R 2 4 π 2 ⇒ k 2 = 8 π 2 3 ⇒ k ≃ 5 , 13


a) Chu vi hình vuông là: 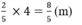
Diện tích hình vuông là: 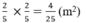
b) Diện tích mỗi ô vuông là: 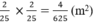
Số hình vuông nhỏ là: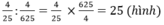
c) Chiều rộng hình chữ nhật là: 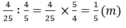
Đáp số: Chu vi hình vuông: 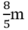
Số hình vuông nhỏ: 25 hình
Chiều rộng hình chữ nhật : 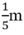
Chọn A
Đặt , ta có:
, ta có: 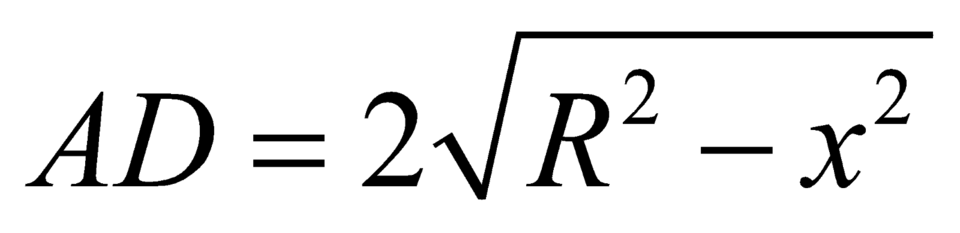 .
.
Dấu bằng xảy ra khi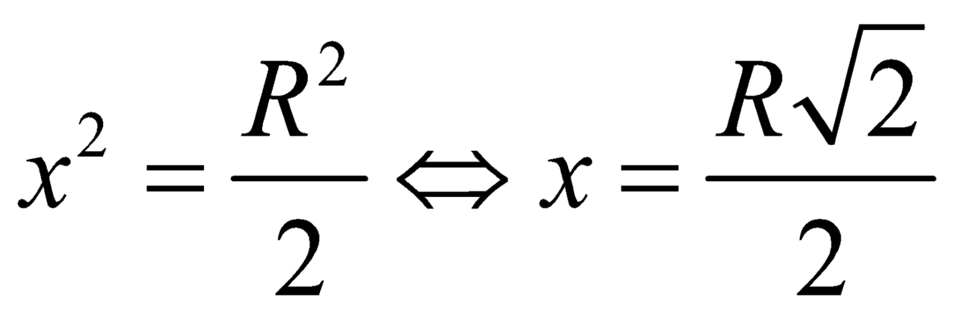 .
.