Có bao nhiêu cách bỏ đồng thời 7 quả bóng bàn giống nhau vào 4 hộp khác nhau sao cho mỗi hộp có ít nhất 1 quả?
A. A 7 3
B. 20
C. 12
D. C 7 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

các đáp án sai hết rùi
Nếu 2 hộp thì mỗi thùng có 42 quả bóng và dư 1 quả (loại)
Nếu 7 hộp thì mỗi thùng có 12 quả bóng và dư 1 quả (loại)
Nếu 4 hộp thì mỗi thùng có 21 quả bóng và dư 1 quả (loại)
Nếu 5 hộp thì mỗi thùng có 17 quả bóng (loại)
Nếu 6 hộp thì mỗi thùng có 14 quả bóng và dư 1 quả (loại)
=>Số hộp ít nhất để có số lượng bóng bằng nhau:
85:7=12 dư1
Vậy có ít nhất 12 cái hộp

mỗi hộp bóng bàn đựng là :
77 : 7 = 11 ( quả )
Đ/S : 11 quả

a, Gọi A là biến cố "Lấy ra bốn quả cùng màu".
\(\Rightarrow\left|\Omega\right|=C^4_{12}\)
\(\left|\Omega_A\right|=C^4_7+C^4_5\)
\(\Rightarrow P\left(A\right)=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{C^4_7+C^4_5}{C^4_{12}}=\dfrac{8}{99}\)
b, Gọi B là biến cố "Lấy ra một quả màu đen".
\(\Rightarrow\overline{B}\) là biến cố "Không lấy ra quả màu đen nào".
\(\Rightarrow\left|\Omega\right|=C^4_{12}\)
\(\left|\Omega_{\overline{B}}\right|=C^4_7\)
\(\Rightarrow P\left(\overline{B}\right)=\dfrac{C^4_7}{C^4_{12}}=\dfrac{7}{99}\)
\(\Rightarrow P\left(B\right)=1-P\left(\overline{B}\right)=\dfrac{92}{99}\)

a) Trong trường hợp này, số cách đặt bằng số các nghiệm
(
x
1
,
x
2
,
x
3
)
nguyên, không âm của phương trình
x
1
+
x
2
+
x
3
=
3
. Từ đó, đáp số cần tìm là 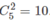
b) Quả thứ nhất có 3 cách đặt;
Quả thứ hai có 3 cách đặt;
Quả thứ ba có 3 cách đặt.
Vậy số cách đặt là 3 3 = 27 .

Đáp án: 66 quả bóng.
Nhận xét: Số lượng bóng chắc chắn là một số không chứa chữ số 8 ở hàng chục vì chỉ có 100 quả, nếu một hộp chứa hơn 80 quả thì số bóng còn lại sẽ không đủ chia cho 4 hộp còn lại theo yêu cầu của đề bài.
Chữ số 8 đó sẽ xuất hiện ở hàng đơn vị. Có 5 hộp nên sẽ có 5 số chứa chữ số 8 ở hàng đơn vị. Từ đó suy ra phần chục sẽ là 100 - 8x5 = 60.
Từ dữ kiện hai hộp có số bóng bằng nhau, ta suy ra một trường hợp duy nhất với số bóng lần lượt ở 5 hộp là 8; 8; 18; 28 và 38 quả bóng.
Như vậy, tổng số bóng trong hai hộp nhiều bóng nhất là 28 + 38 = 66 quả bóng.

a) Trong trường hợp này, số cách đặt bằng số các nghiệm \(\left(x_1,x_2,x_3\right)\) nguyên, không âm của phương trình \(x_1+x_2+x_3=3\). Từ đó, đáp số cần tìm là \(C^2_5=10\)
b) Quả thứ nhất có 3 cách đặt
Quả thứ hai có 3 cách đặt
Quả thứ ba có 3 cách đặt
Vậy số cách đặt là \(3^3=27\)

câu 1
- Nếu bạn đưa nốt 1.000 cho bố hoặc mẹ thì bạn chỉ còn nợ bố và mẹ: 98.000 - 1.000 = 97.000 - bằng giá trị cái váy bạn mua.
- Nếu bạn giữ lại 1.000 và 97.000 giá trị cái váy sẽ có tổng là 98.000, bằng số tiền nợ bố mẹ
Do đó, bạn sẽ không bị mất đồng nào
câu 3
Đầu tiên A qua với B mất 2 phút, A quay lại mất 1 phút, A qua với C mất 7 phút, A quay về mất 1 phút, A qua với D mất 10 phút.
Tổng cộng 21 phút.
Chọn B
Đặt 7 quả bóng trên bàn, giữa 7 quả bóng có 6 khoảng trống. Ta muốn chia làm 4 phần thì ta dùng 3cái que, ta đặt vào 3 trong 6 khoảng trống, ta có C 6 3 cách đt.
Do đó số cách chia 7 quả bóng thành 4 phần để bỏ vào 4 hộp khác nhau sao cho mỗi hộp có ít nhất 1 quả là: C 6 3 = 20 cách