Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Để ý rằng OH nằm trong mặt phẳng (OAB) và OH vuông góc với AB, nên một vecto chỉ phương của OH là tích có hướng của A B → và vecto pháp tuyến của mặt phẳng (OAB).
Đáp án A
Ta có: A B → 2 ; 1 ; 0 , O B → 1 ; 0 ; 0 ⇒ d O , A B = A B → ; O B → A B → = 1 5
Đáp án A
Phương pháp:
Công thức khoảng cách từ điểm đến đường thẳng trong không gian:
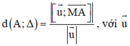là VTCP của Δ và M là điểm bất kì thuộc
Cách giải:
Độ dài đường cao kẻ từ O của tam giác OAB bằng khoảng cách từ O đến đường thẳng AB:
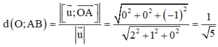
(S) có tâm I ( 2;2;2 ), bán kính R = 2 3 . Nhận thấy O và A đều thuộc (S). Tam giác OAB đều, có bán kính đường tròn ngoại tiếp r = O A 3 = 4 2 3
Khoảng cách d ( I; (P) ) = R 2 - r 2 = 2 3
(P) đi qua O có phương trình dạng: ax + by +cz = 0
(P) đi qua A, suy ra b = -a
d ( I; (P) ) = 2 3 ⇔ 2 a + b + c a 2 + b 2 + c 2 = 2 3
⇔ 2 c 2 a 2 + c 2 = 2 3 ⇔ 4 c 2 2 a 2 + c 2 = 4 3 ⇔ 12 c 2 = 8 a 2 + 4 c 2 ⇔ c 2 = a 2 ⇔ c = ± a
Vậy có hai mặt phẳng cần tìm: x - y + z = 0; x - y - z = 0
Đáp án B
Đáp án C.
Đặt B x ; y ; z . Ta có O A 2 = 8, Δ O A B đều ⇒ O A 2 = O B 2 = A B 2 = 8 .
Mà B ∈ S ⇒ Ta có hệ x 2 + y 2 + z 2 − 2 x − 2 y − 2 z = 0 1 x 2 + y 2 + z 2 = 8 (2) x − 2 2 + y − 2 2 + z 2 = 8 (3)
Thế (2) vào (1) và (3) ta được: x + y + z = 4 x + y = 2 ⇔ z = 2 y = 2 − x .
Thế vào (2):
x 2 + 2 − x 2 = 8 ⇔ 2 x 2 − 4 x = 0 ⇔ x = 0 l x = 2
Với x = 2 ⇒ y = 0 ⇒ B 2 ; 0 ; 2
⇒ n → = O A → , O B → = 4 ; − 4 ; − 4 ⇒ Phương trình O A B : x − y − z = 0 .
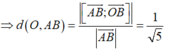
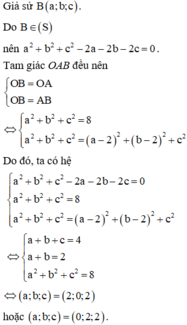
Đáp án D
Để ý rằng OH nằm trong mặt phẳng (OAB) và OH vuông góc với AB, nên một vecto chỉ phương của OH là tích có hướng của A B → và vecto pháp tuyến của mặt phẳng (OAB).