Thầy Tuấn có 15 cuốn sách gồm 4 cuốn sách Toán , 5 cuốn sách Lý và 6 cuốn sách Hóa. Các cuốn sách đôi một khác nhau. Thầy chọn ngẫu nhiên 8 cuốn sách để làm phầnt hưởng cho một học sinh. Tính xác suất để số cuốn sách còn lại thầy Tuấn còn đủ 3 môn
A. 54 715
B. 661 715
C. 2072 2145
D. 73 2145

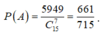

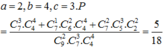
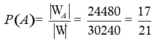
Đáp án B
Gọi biến cố A: “Số cuốn sách còn lại của thầy Tuấn có đủ cả ba môn”.
Khi đó ta có biến cố: A ¯ : “Số cuốn sách còn lại của thầy Tuấn không có đủ cả 3 môn”.