Từ các chữ số {0;1;2;3;4} lập được tất cả bao nhiêu số chẵn có 4 chữ số khác nhau sao cho chữ số 2 và 3 đứng cạnh nhau.
A. 20
B. 16
C. 14
D. 18
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
2 tháng 3 2016
-Có 10 cách chọn chữ số làm tử số
-Có 9 cách chọn chữ số làm mẫu số
Có số phân số lập được từ các chữ số đã cho là:10*9=90(phân số)
Đáp số:90 phân số
9 tháng 7 2016
Số lập được có dạng 0,abc .
Các số lập được là :
0,123
0,132
0,231
0,213
0,321
0,312
Sắp xếp :
0,123
0,132
0,213
0,231
0,312
0,321
30 tháng 10 2021
, Từ các chữ số đó ,hãy viết các số thập phân bé hơn 1 mà mỗi số có đủ cả bốn chữ số đó
. b, Tính tổng của các số thập phân đó. (bằng cách thuận tiện nhất) a.0,123 0,132 0,213 0,231 0,312 0,321 b.0,123 + 0,132 + 0,213 + 0,231 + 0,312 + 0,321 = (0,123 + 0,132 ) + (0,213 + 0,312) + ( 0,231 + 0,321) = (0,255 + 0,525) + 0,552 = 0,78 + 0,552
NK
10
Các bạn bạn nào biết giải bài này bằng lời giải và phép tính thì giúp mình với. Mình cảm ơn 
9 tháng 7 2023
a: \(\overline{abc}\)
a có 3 cáhc
b có 4 cáhc
c có 4 cách
=>Có 3*4*4=48 cách
b: \(\overline{abcd}\)
a có 3 cách
b có 3 cách
c có 2 cách
d có 1 cách
=>Có 3*3*2=18 cách
c: \(\overline{abc}\)
c có 1 cách
a có 3 cách
b có 4 cách
=>Có 1*3*4=12 cách
d: \(\overline{abcd}\)
TH1: d=0
=>Có 3*4*4=48 cách
TH2: d<>0
d có 2 cách
a có 3 cách
b có 4 cách
c có 4 cách
=>Có 4*4*3*2=16*6=96 cách
=>Có 144 cách
3 tháng 4 2017
a,Các số tự nhiên có 3 chữ số , mỗi số có đủ 3 chữ số 1;2;0 được sắp xếp theo thứ tự từ bé đến lớn là : 102;120;201;210.
b,Các số thập phân có 3 chữ số , mỗi số có đủ 3 chữ số 1;2;0 và phần nguyên có 1 chữ số là : 0,12;0,21;1,02;1,20;2,01;2,10.
9 tháng 4 2018
a,Các số tự nhiên có 3 chữ số , mỗi số có đủ 3 chữ số 1;2;0 được sắp xếp theo thứ tự từ bé đến lớn là : 102;120;201;210.
b,Các số thập phân có 3 chữ số , mỗi số có đủ 3 chữ số 1;2;0 và phần nguyên có 1 chữ số là : 0,12;0,21;1,02;1,20;2,01;2,10.
@_@
DD
Đoàn Đức Hà
Giáo viên
8 tháng 5 2021
Số \(2000020\)có chữ số \(2\)xuất hiện ở vị trí thứ \(7\)và vị trí thứ \(2\)nên nó xuất hiện ở vị trí thứ:
\(2\times2\times...\times2\)(\(6\)chữ số \(2\)) \(+2=64+2=66\).
24 tháng 8 2016
a. 10,18, 30, 38, 50, 58, 70, 78.
b. 13, 15, 17, 31, 35, 37, 51, 53, 57, 71, 73, 75.
Chọn D
Gọi số cần tìm có dạng
là các số thuộc tập hợp {0;1;2;3;4}
Vì chữ số 2 và 3 đứng cạnh nhau và số lập được là chẵn nên ta có các trường hợp như sau:
TH1: Số có dạng
+ Chọn d có 2 cách.
+ Chọn c có 2 cách.
Vậy có 2.2.2 = 8 kết quả của TH1.
TH2: Số có dạng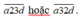
* Nếu d = 0 thì chọn a có 2 cách.
* Nếu d = 4 thì chọn a có 1 cách.
Vậy có 2.(1+2) = 6 kết quả của TH2.
TH5: Số có dạng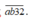
+ Chọn a có 2 cách.
+ Chọn b có 2 cách.
Vậy có 2.2 = 4 kết quả của TH5.
Vậy có tất cả 8 + 6 + 4 = 18 kết quả thỏa mãn.