Đặt T là tổng bình phương tất cả các nghiệm của phương trình
1
6
−
log
2
4
x
+
2
2
+
log
2
x
=
1.
Vậy T bằng
A. 6
B. 20
C. 36
D. 2


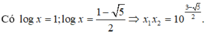
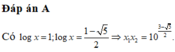

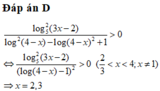
Đáp án B
Điều kiện:
x > 0 log 2 4 x ≠ 6 log 2 x ≠ − 2 ⇔ x > 0 x ≠ 16 x ≠ 1 4 .
1 6 − log 2 4 x + 2 2 + log 2 x = 1 ⇔ 1 4 − log 2 x + 2 2 + log 2 x = 1 ⇔ 2 + log 2 x + 8 − 2 log 2 x 4 − log 2 x 2 + log 2 x = 1 ⇔ 10 − log 2 x = − log 2 2 x + 2 log 2 x + 8 ⇔ − log 2 2 x + 3 log 2 x − 2 = 0 ⇔ log 2 x = 1 log 2 x = 2 ⇔ x = 2 x = 4 .
Vậy tổng bình phương tất cả các nghiệm của phương trình bằng 20